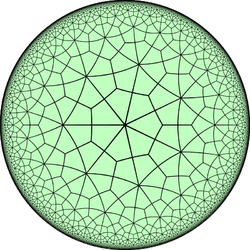
Truncated triheptagonal tiling
| Truncated triheptagonal tiling | |
|---|---|
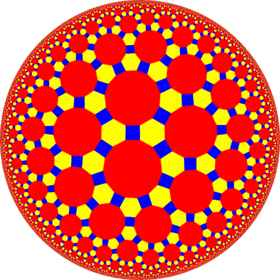 Poincaré disk model of the hyperbolic plane | |
| Type | Hyperbolic uniform tiling |
| Vertex configuration | 4.6.14 |
| Schläfli symbol | tr{7,3} or |
| Wythoff symbol | 2 7 3 | |
| Coxeter diagram | |
| Symmetry group | [7,3], (*732) |
| Dual | Order 3-7 kisrhombille |
| Properties | Vertex-transitive |
In geometry, the truncated triheptagonal tiling is a semiregular tiling of the hyperbolic plane. There are one square, one hexagon, and one tetradecagon (14-sides) on each vertex. It has Schläfli symbol of tr{7,3}.
Uniform colorings
There is only one uniform coloring of a truncated triheptagonal tiling. (Naming the colors by indices around a vertex: 123.)
Symmetry
Each triangle in this dual tiling, order 3-7 kisrhombille, represent a fundamental domain of the Wythoff construction for the symmetry group [7,3].
 |
 | |
| The dual tiling is called an order-3 bisected heptagonal tiling, made as a complete bisection of the heptagonal tiling, here shown with triangles with alternating colors. | ||
Related polyhedra and tilings
This tiling can be considered a member of a sequence of uniform patterns with vertex figure (4.6.2p) and Coxeter-Dynkin diagram ![]()
![]()
![]()
![]()
![]() . For p < 6, the members of the sequence are omnitruncated polyhedra (zonohedrons), shown below as spherical tilings. For p > 6, they are tilings of the hyperbolic plane, starting with the truncated triheptagonal tiling.
. For p < 6, the members of the sequence are omnitruncated polyhedra (zonohedrons), shown below as spherical tilings. For p > 6, they are tilings of the hyperbolic plane, starting with the truncated triheptagonal tiling.
| *n32 symmetry mutations of omnitruncated tilings: 4.6.2n | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Sym. *n32 [n,3] |
Spherical | Euclid. | Compact hyperb. | Paraco. | Noncompact hyperbolic | |||||||
| *232 [2,3] |
*332 [3,3] |
*432 [4,3] |
*532 [5,3] |
*632 [6,3] |
*732 [7,3] |
*832 [8,3] |
*∞32 [∞,3] |
[12i,3] |
[9i,3] |
[6i,3] |
[3i,3] | |
| Figures |  |
 |
 |
 |
 |
 |
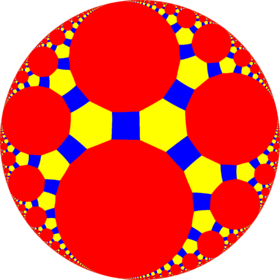 |
 |
 |
 |
 | |
| Config. | 4.6.4 | 4.6.6 | 4.6.8 | 4.6.10 | 4.6.12 | 4.6.14 | 4.6.16 | 4.6.∞ | 4.6.24i | 4.6.18i | 4.6.12i | 4.6.6i |
| Duals |  |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
| Config. | V4.6.4 | V4.6.6 | V4.6.8 | V4.6.10 | V4.6.12 | V4.6.14 | V4.6.16 | V4.6.∞ | V4.6.24i | V4.6.18i | V4.6.12i | V4.6.6i |
From a Wythoff construction there are eight hyperbolic uniform tilings that can be based from the regular heptagonal tiling.
Drawing the tiles colored as red on the original faces, yellow at the original vertices, and blue along the original edges, there are 8 forms.
| Uniform heptagonal/triangular tilings | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Symmetry: [7,3], (*732) | [7,3]+, (732) | ||||||||||
 |
 |
 |
 |
 |
 |
 |
 | ||||
| {7,3} | t{7,3} | r{7,3} | t{3,7} | {3,7} | rr{7,3} | tr{7,3} | sr{7,3} | ||||
| Uniform duals | |||||||||||
 |
 |
 |
 |
 |
 |
 |
 | ||||
| V73 | V3.14.14 | V3.7.3.7 | V6.6.7 | V37 | V3.4.7.4 | V4.6.14 | V3.3.3.3.7 | ||||
See also
| Wikimedia Commons has media related to Uniform tiling 4-6-14. |
References
- John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, The Symmetries of Things 2008, ISBN 978-1-56881-220-5 (Chapter 19, The Hyperbolic Archimedean Tessellations)
- "Chapter 10: Regular honeycombs in hyperbolic space". The Beauty of Geometry: Twelve Essays. Dover Publications. 1999. ISBN 0-486-40919-8. LCCN 99035678.
External links
- Hyperbolic and Spherical Tiling Gallery
- KaleidoTile 3: Educational software to create spherical, planar and hyperbolic tilings
- Hyperbolic Planar Tessellations, Don Hatch
