Square tiling
| Square tiling | |
|---|---|
 | |
| Type | Regular tiling |
| Vertex configuration | 4.4.4.4 (or 44) |
| Schläfli symbol(s) | {4,4} {∞}×{∞} |
| Wythoff symbol(s) | 4 | 2 4 |
| Coxeter diagram(s) | |
| Symmetry | p4m, [4,4], (*442) |
| Rotation symmetry | p4, [4,4]+, (442) |
| Dual | self-dual |
| Properties | Vertex-transitive, edge-transitive, face-transitive |
In geometry, the square tiling, square tessellation or square grid is a regular tiling of the Euclidean plane. It has Schläfli symbol of {4,4}, meaning it has 4 squares around every vertex.
Conway calls it a quadrille.
The internal angle of the square is 90 degrees so four squares at a point make a full 360 degrees. It is one of three regular tilings of the plane. The other two are the triangular tiling and the hexagonal tiling.
Uniform colorings
There are 9 distinct uniform colorings of a square tiling. Naming the colors by indices on the 4 squares around a vertex: 1111, 1112(i), 1112(ii), 1122, 1123(i), 1123(ii), 1212, 1213, 1234. (i) cases have simple reflection symmetry, and (ii) glide reflection symmetry. Three can be seen in the same symmetry domain as reduced colorings: 1112i from 1213, 1123i from 1234, and 1112ii reduced from 1123ii.
| 9 uniform colorings | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1111 | 1212 | 1213 | 1112i | 1122 | |||||||
 |
 |
 |
 |
 | |||||||
| p4m (*442) | p4m (*442) | pmm (*2222) | |||||||||
| 1234 | 1123i | 1123ii | 1112ii | ||||||||
 |
 |
 |
 | ||||||||
| pmm (*2222) | cmm (2*22) | ||||||||||
Related polyhedra and tilings
This tiling is topologically related as a part of sequence of regular polyhedra and tilings, extending into the hyperbolic plane: {4,p}, p=3,4,5...
| *n42 symmetry mutation of regular tilings: {4,n} | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Spherical | Euclidean | Compact hyperbolic | Paracompact | ||||||||
 {4,3} |
 {4,4} |
 {4,5} |
 {4,6} |
 {4,7} |
 {4,8}... |
 {4,∞} | |||||
This tiling is also topologically related as a part of sequence of regular polyhedra and tilings with four faces per vertex, starting with the octahedron, with Schläfli symbol {n,4}, and Coxeter diagram ![]()
![]()
![]()
![]()
![]() , with n progressing to infinity.
, with n progressing to infinity.
| *n42 symmetry mutation of regular tilings: {n,4} | |||||||
|---|---|---|---|---|---|---|---|
| Spherical | Euclidean | Hyperbolic tilings | |||||
 |
 |
 |
 |
 |
 |
 | |
| 24 | 34 | 44 | 54 | 64 | 74 | 84 | ...∞4 |
| *n42 symmetry mutations of quasiregular dual tilings: V(4.n)2 | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Symmetry *4n2 [n,4] |
Spherical | Euclidean | Compact hyperbolic | Paracompact | Noncompact | ||||||
| *342 [3,4] |
*442 [4,4] |
*542 [5,4] |
*642 [6,4] |
*742 [7,4] |
*842 [8,4]... |
*∞42 [∞,4] |
[iπ/λ,4] | ||||
| Tiling Conf. |
 V4.3.4.3 |
 V4.4.4.4 |
 V4.5.4.5 |
 V4.6.4.6 |
 V4.7.4.7 |
 V4.8.4.8 |
 V4.∞.4.∞ |
V4.∞.4.∞ | |||
| *n42 symmetry mutation of expanded tilings: n.4.4.4 | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Symmetry [n,4], (*n42) |
Spherical | Euclidean | Compact hyperbolic | Paracomp. | |||||||
| *342 [3,4] |
*442 [4,4] |
*542 [5,4] |
*642 [6,4] |
*742 [7,4] |
*842 [8,4] |
*∞42 [∞,4] | |||||
| Expanded figures |
 |
 |
 |
 |
 |
 |
 | ||||
| Config. | 3.4.4.4 | 4.4.4.4 | 5.4.4.4 | 6.4.4.4 | 7.4.4.4 | 8.4.4.4 | ∞.4.4.4 | ||||
| Rhombic figures config. |
 V3.4.4.4 |
 V4.4.4.4 |
 V5.4.4.4 |
 V6.4.4.4 |
 V7.4.4.4 |
 V8.4.4.4 |
 V∞.4.4.4 | ||||
Wythoff constructions from square tiling
Like the uniform polyhedra there are eight uniform tilings that can be based from the regular square tiling.
Drawing the tiles colored as red on the original faces, yellow at the original vertices, and blue along the original edges, all 8 forms are distinct. However treating faces identically, there are only three topologically distinct forms: square tiling, truncated square tiling, snub square tiling.
| Uniform tilings based on square tiling symmetry | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Symmetry: [4,4], (*442) | [4,4]+, (442) | [4,4+], (4*2) | |||||||||
 |
 |
 |
 |
 |
 |
 |
 | ||||
| {4,4} | t{4,4} | r{4,4} | t{4,4} | {4,4} | rr{4,4} | tr{4,4} | sr{4,4} | s{4,4} | |||
| Uniform duals | |||||||||||
 |
 |
 |
 |
 |
 |
 |
 | ||||
| V4.4.4.4 | V4.8.8 | V4.4.4.4 | V4.8.8 | V4.4.4.4 | V4.4.4.4 | V4.8.8 | V3.3.4.3.4 | ||||
Topologically equivalent tilings


Other quadrilateral tilings can be made with topologically equivalent to the square tiling (4 quads around every vertex).
Isohedral tilings have identical faces (face-transitivity) and vertex-transitivity, there are 17 variations, with 6 identified as triangles that do not connect edge-to-edge, or as quadrilateral with two colinear edges. Symmetry given assumes all faces are the same color.[1]
 |
 |
 |
 |
 |
 |
| Square p4m, (*442) |
Rectangle pmm, (*2222) |
Parallelogram p2, (2222) |
Parallelogram pmg, (22*) |
Rhombus cmm, (2*22) |
Rhombus pmg, (22*) |
|---|---|---|---|---|---|
 |
 |
 |
 |
 |
 |
| Trapezoid cmm, (2*22) |
Quadrilateral pgg, (22×) |
Kite pmg, (22*) |
Quadrilateral pgg, (22×) |
Quadrilateral p2, (2222) | |
 |
 |
 |
 |
 |
 |
| Isosceles pmg, (22*) |
Isosceles pgg, (22×) |
Scalene pgg, (22×) |
Scalene p2, (2222) | ||
|---|---|---|---|---|---|
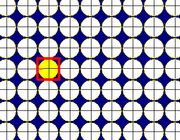
Circle packing
The square tiling can be used as a circle packing, placing equal diameter circles at the center of every point. Every circle is in contact with 4 other circles in the packing (kissing number).[2] The packing density is π/4=78.54% coverage. There are 4 uniform colorings of the circle packings.
 |
 |
 |
 |
Related regular complex apeirogons
There are 3 regular complex apeirogons, sharing the vertices of the square tiling. Regular complex apeirogons have vertices and edges, where edges can contain 2 or more vertices. Regular apeirogons p{q}r are contrained by: 1/p + 2/q + 1/r = 1. Edges have p vertices, and vertex figures are r-gonal.[3]
| Self-dual | Duals | |
|---|---|---|
 |
 |
 |
| 4{4}4 or |
2{8}4 or |
4{8}2 or |
See also
| Wikimedia Commons has media related to Order-4 square tiling. |
- Checkerboard
- List of regular polytopes
- List of uniform tilings
- Square lattice
- Tilings of regular polygons
References
- Coxeter, H.S.M. Regular Polytopes, (3rd edition, 1973), Dover edition, ISBN 0-486-61480-8 p. 296, Table II: Regular honeycombs
- Klitzing, Richard. "2D Euclidean tilings o4o4x - squat - O1".
- Williams, Robert (1979). The Geometrical Foundation of Natural Structure: A Source Book of Design. Dover Publications, Inc. ISBN 0-486-23729-X. p36
- Grünbaum, Branko ; and Shephard, G. C. (1987). Tilings and Patterns. New York: W. H. Freeman. ISBN 0-7167-1193-1. (Chapter 2.1: Regular and uniform tilings, p. 58-65)
- John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, The Symmetries of Things 2008, ISBN 978-1-56881-220-5
External links
| Fundamental convex regular and uniform honeycombs in dimensions 3–10 (or 2-9) | |||||
|---|---|---|---|---|---|
| Family | / / | ||||
| Uniform tiling | {3[3]} | δ3 | hδ3 | qδ3 | Hexagonal |
| Uniform convex honeycomb | {3[4]} | δ4 | hδ4 | qδ4 | |
| Uniform 5-honeycomb | {3[5]} | δ5 | hδ5 | qδ5 | 24-cell honeycomb |
| Uniform 6-honeycomb | {3[6]} | δ6 | hδ6 | qδ6 | |
| Uniform 7-honeycomb | {3[7]} | δ7 | hδ7 | qδ7 | 222 |
| Uniform 8-honeycomb | {3[8]} | δ8 | hδ8 | qδ8 | 133 • 331 |
| Uniform 9-honeycomb | {3[9]} | δ9 | hδ9 | qδ9 | 152 • 251 • 521 |
| Uniform 10-honeycomb | {3[10]} | δ10 | hδ10 | qδ10 | |
| Uniform n-honeycomb | {3[n]} | δn | hδn | qδn | 1k2 • 2k1 • k21 |
