Hosohedron
| Set of regular n-gonal hosohedra | |
|---|---|
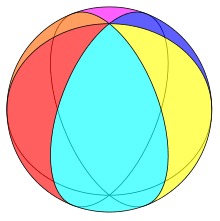 Example hexagonal hosohedron on a sphere | |
| Type | Regular polyhedron or spherical tiling |
| Faces | n digons |
| Edges | n |
| Vertices | 2 |
| χ | 2 |
| Vertex configuration | 2n |
| Wythoff symbol | n | 2 2 |
| Schläfli symbol | {2,n} |
| Coxeter diagram |
|
| Symmetry group | Dnh, [2,n], (*22n), order 4n |
| Rotation group | Dn, [2,n]+, (22n), order 2n |
| Dual polyhedron | dihedron |

In geometry, an n-gonal hosohedron is a tessellation of lunes on a spherical surface, such that each lune shares the same two polar opposite vertices.
A regular n-gonal hosohedron has Schläfli symbol {2, n}, with each spherical lune having internal angle 2π/n radians (360°/n).[1][2]
Hosohedra as regular polyhedra
For a regular polyhedron whose Schläfli symbol is {m, n}, the number of polygonal faces may be found by:
The Platonic solids known to antiquity are the only integer solutions for m ≥ 3 and n ≥ 3. The restriction m ≥ 3 enforces that the polygonal faces must have at least three sides.
When considering polyhedra as a spherical tiling, this restriction may be relaxed, since digons (2-gons) can be represented as spherical lunes, having non-zero area. Allowing m = 2 admits a new infinite class of regular polyhedra, which are the hosohedra. On a spherical surface, the polyhedron {2, n} is represented as n abutting lunes, with interior angles of 2π/n. All these lunes share two common vertices.
 A regular trigonal hosohedron, {2,3}, represented as a tessellation of 3 spherical lunes on a sphere. |
 A regular tetragonal hosohedron, represented as a tessellation of 4 spherical lunes on a sphere. |
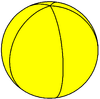
| n | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12... |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Image |  |
 |
 |
 |
 |
 |
 |
 |
 |
 | |
| {2,n} | {2,2} | {2,3} | {2,4} | {2,5} | {2,6} | {2,7} | {2,8} | {2,9} | {2,10} | {2,11} | {2,12} |
| Coxeter |
Kaleidoscopic symmetry
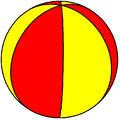
The digonal (lune) faces of a 2n-hosohedron, {2,2n}, represents the fundamental domains of dihedral symmetry in three dimensions: Cnv, [n], (*nn), order 2n. The reflection domains can be shown as alternately colored lunes as mirror images. Bisecting the lunes into two spherical triangles creates bipyramids and define dihedral symmetry Dnh, order 4n.
| Symmetry | C1v, [ ] | C2v, [2] | C3v, [3] | C4v, [4] | C5v, [5] | C6v, [6] |
|---|---|---|---|---|---|---|
| Hosohedron | {2,2} | {2,4} | {2,6} | {2,8} | {2,10} | {2,12} |
| Fundamental domains |  |
 |
 |
 |
 |
 |
Relationship with the Steinmetz solid
The tetragonal hosohedron is topologically equivalent to the bicylinder Steinmetz solid, the intersection of two cylinders at right-angles.[3]
Derivative polyhedra
The dual of the n-gonal hosohedron {2, n} is the n-gonal dihedron, {n, 2}. The polyhedron {2,2} is self-dual, and is both a hosohedron and a dihedron.
A hosohedron may be modified in the same manner as the other polyhedra to produce a truncated variation. The truncated n-gonal hosohedron is the n-gonal prism.
Apeirogonal hosohedron
In the limit the hosohedron becomes an apeirogonal hosohedron as a 2-dimensional tessellation:
Hosotopes
Multidimensional analogues in general are called hosotopes. A regular hosotope with Schläfli symbol {2,p,...,q} has two vertices, each with a vertex figure {p,...,q}.
The two-dimensional hosotope, {2}, is a digon.
Etymology
The term “hosohedron” was coined by H.S.M. Coxeter, and possibly derives from the Greek ὅσος (hosos) “as many”, the idea being that a hosohedron can have “as many faces as desired”.[4]
See also
| Wikimedia Commons has media related to Hosohedra. |
References
- ↑ Coxeter, Regular polytopes, p. 12
- ↑ Abstract Regular polytopes, p. 161
- ↑ Weisstein, Eric W. "Steinmetz Solid". MathWorld.
- ↑ Steven Schwartzman (1 January 1994). The Words of Mathematics: An Etymological Dictionary of Mathematical Terms Used in English. MAA. pp. 108–109. ISBN 978-0-88385-511-9.
- McMullen, Peter; Schulte, Egon (December 2002), Abstract Regular Polytopes (1st ed.), Cambridge University Press, ISBN 0-521-81496-0
- Coxeter, H.S.M; Regular Polytopes (third edition). Dover Publications Inc. ISBN 0-486-61480-8

