Truncated octahedron
| Truncated octahedron | |
|---|---|
 (Click here for rotating model) | |
| Type | Archimedean solid Uniform polyhedron |
| Elements | F = 14, E = 36, V = 24 (χ = 2) |
| Faces by sides | 6{4}+8{6} |
| Conway notation | tO bT |
| Schläfli symbols | t{3,4} tr{3,3} or |
| t0,1{3,4} or t0,1,2{3,3} | |
| Wythoff symbol | 2 4 | 3 3 3 2 | |
| Coxeter diagram | |
| Symmetry group | Oh, B3, [4,3], (*432), order 48 Th, [3,3] and (*332), order 24 |
| Rotation group | O, [4,3]+, (432), order 24 |
| Dihedral Angle | 4-6: arccos(−1/√3) = 125°15′51″ 6-6: arccos(−1/3) = 109°28′16″ |
| References | U08, C20, W7 |
| Properties | Semiregular convex parallelohedron permutohedron |
 Colored faces |
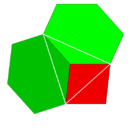 4.6.6 (Vertex figure) |
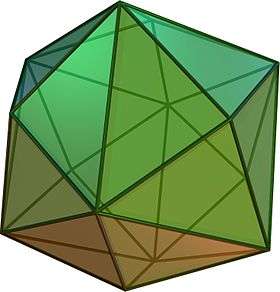 Tetrakis hexahedron (dual polyhedron) |
 Net |
In geometry, the truncated octahedron is an Archimedean solid. It has 14 faces (8 regular hexagonal and 6 square), 36 edges, and 24 vertices. Since each of its faces has point symmetry the truncated octahedron is a zonohedron. It is also the Goldberg polyhedron GIV(1,1), containing square and hexagonal faces. Like the cube, it can tessellate (or "pack") 3-dimensional space, as a permutohedron.
Its dual polyhedron is the tetrakis hexahedron.
If the original truncated octahedron has unit edge length, its dual tetrakis cube has edge lengths 9/8√2 and 3/2√2.
Construction
 |
 |
A truncated octahedron is constructed from a regular octahedron with side length 3a by the removal of six right square pyramids, one from each point. These pyramids have both base side length (a) and lateral side length (e) of a, to form equilateral triangles. The base area is then a2. Note that this shape is exactly similar to half an octahedron or Johnson solid J1.
From the properties of square pyramids, we can now find the slant height, s, and the height, h, of the pyramid:
The volume, V, of the pyramid is given by:
Because six pyramids are removed by truncation, there is a total lost volume of √2a3.
Orthogonal projections
The truncated octahedron has five special orthogonal projections, centered, on a vertex, on two types of edges, and two types of faces: Hexagon, and square. The last two correspond to the B2 and A2 Coxeter planes.
| Centered by | Vertex | Edge 4-6 |
Edge 6-6 |
Face Square |
Face Hexagon |
|---|---|---|---|---|---|
| Truncated octahedron |
 |
 |
 |
 |
 |
| Hexakis hexahedron |
 |
 |
 |
 |
 |
| Projective symmetry |
[2] | [2] | [2] | [4] | [6] |
Spherical tiling
The truncated octahedron can also be represented as a spherical tiling, and projected onto the plane via a stereographic projection. This projection is conformal, preserving angles but not areas or lengths. Straight lines on the sphere are projected as circular arcs on the plane.
 |
 square-centered |
 hexagon-centered |
| Orthographic projection | Stereographic projections | |
|---|---|---|
Coordinates
 |
 |
| Orthogonal projection in bounding box (±2,±2,±2) |
Truncated octahedron with hexagons replaced by 6 coplanar triangles. There are 8 new vertices at: (±1,±1,±1). |
All permutations of (0, ±1, ±2) are Cartesian coordinates of the vertices of a truncated octahedron of edge length a = √ 2 centered at the origin. The vertices are thus also the corners of 12 rectangles whose long edges are parallel to the coordinate axes.
The edge vectors have Cartesian coordinates (0, ±1, ±1) and permutations of these. The face normals (normalized cross products of edges that share a common vertex) of the 6 square faces are (0, 0, ±1), (0, ±1, 0) and (±1, 0, 0). The face normals of the 8 hexagonal faces are (±1/√3, ±1/√3, ±1/√3). The dot product between pairs of two face normals is the cosine of the dihedral angle between adjacent faces, either −1/3 or −1/√3. The dihedral angle is approximately 1.910633 radians (109.471° ![]() A156546) at edges shared by two hexagons or 2.186276 radians (125.263°
A156546) at edges shared by two hexagons or 2.186276 radians (125.263° ![]() A195698) at edges shared by a hexagon and a square.
A195698) at edges shared by a hexagon and a square.
Dissection
The truncated octahedron can be dissected into a central octahedron, surrounded by 8 triangular cupola on each face, and 6 square pyramids above the vertices.[1]
Removing the central octahedron and 2 or 4 triangular cupola creates two Stewart toroids, with dihedral and tetrahedral symmetry:
| Genus 2 | Genus 3 |
|---|---|
| D3d, [2+,6], (2*3), order 12 | Td, [3,3], (*332), order 24 |
 |
 |
Permutohedron
The truncated octahedron can also be represented by even more symmetric coordinates in four dimensions: all permutations of (1, 2, 3, 4) form the vertices of a truncated octahedron in the three-dimensional subspace x + y + z + w = 10. Therefore, the truncated octahedron is the permutohedron of order 4: each vertex corresponds to a permutation of (1, 2, 3, 4) and each edge represents a single pairwise swap of two elements.

Area and volume
The area A and the volume V of a truncated octahedron of edge length a are:
Uniform colorings
There are two uniform colorings, with tetrahedral symmetry and octahedral symmetry, and two 2-uniform coloring with dihedral symmetry as a truncated triangular antiprism. The construcational names are given for each. Their Conway polyhedron notation is given in parentheses.
| 1-uniform | 2-uniform | ||
|---|---|---|---|
| Oh, [4,3], (*432) Order 48 |
Td, [3,3], (*332) Order 24 |
D4h, [4,2], (*422) Order 16 |
D3d, [2+,6], (2*3) Order 12 |
 122 coloring |
 123 coloring |
 122 & 322 colorings |
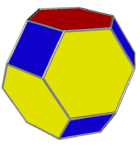 122 & 123 colorings |
| Truncated octahedron (tO) |
Bevelled tetrahedron (bT) |
Truncated square bipyramid (tdP4) |
Truncated triangular antiprism (tA3) |
Related polyhedra
The truncated octahedron is one of a family of uniform polyhedra related to the cube and regular octahedron.
| Uniform octahedral polyhedra | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Symmetry: [4,3], (*432) | [4,3]+ (432) |
[1+,4,3] = [3,3] (*332) |
[3+,4] (3*2) | |||||||
| {4,3} | t{4,3} | r{4,3} r{31,1} |
t{3,4} t{31,1} |
{3,4} {31,1} |
rr{4,3} s2{3,4} |
tr{4,3} | sr{4,3} | h{4,3} {3,3} |
h2{4,3} t{3,3} |
s{3,4} s{31,1} |
= |
= |
= |
||||||||
| Duals to uniform polyhedra | ||||||||||
| V43 | V3.82 | V(3.4)2 | V4.62 | V34 | V3.43 | V4.6.8 | V34.4 | V33 | V3.62 | V35 |
It also exists as the omnitruncate of the tetrahedron family:
| Family of uniform tetrahedral polyhedra | |||||||
|---|---|---|---|---|---|---|---|
| Symmetry: [3,3], (*332) | [3,3]+, (332) | ||||||
 |
 |
 |
 |
 |
 |
 |
 |
| {3,3} | t{3,3} | r{3,3} | t{3,3} | {3,3} | rr{3,3} | tr{3,3} | sr{3,3} |
| Duals to uniform polyhedra | |||||||
 |
 |
 |
 |
 | |||
| V3.3.3 | V3.6.6 | V3.3.3.3 | V3.6.6 | V3.3.3 | V3.4.3.4 | V4.6.6 | V3.3.3.3.3 |
Symmetry mutations
| *n32 symmetry mutations of omnitruncated tilings: 4.6.2n | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Sym. *n32 [n,3] |
Spherical | Euclid. | Compact hyperb. | Paraco. | Noncompact hyperbolic | |||||||
| *232 [2,3] |
*332 [3,3] |
*432 [4,3] |
*532 [5,3] |
*632 [6,3] |
*732 [7,3] |
*832 [8,3] |
*∞32 [∞,3] |
[12i,3] |
[9i,3] |
[6i,3] |
[3i,3] | |
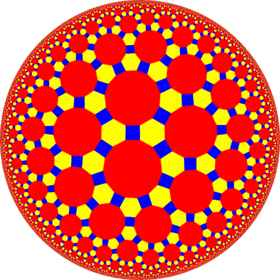
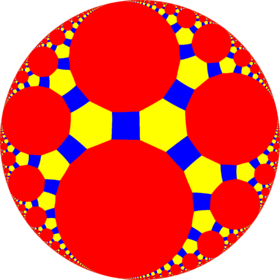
| Figures |  |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 | |
| Config. | 4.6.4 | 4.6.6 | 4.6.8 | 4.6.10 | 4.6.12 | 4.6.14 | 4.6.16 | 4.6.∞ | 4.6.24i | 4.6.18i | 4.6.12i | 4.6.6i |
| Duals |  |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
| Config. | V4.6.4 | V4.6.6 | V4.6.8 | V4.6.10 | V4.6.12 | V4.6.14 | V4.6.16 | V4.6.∞ | V4.6.24i | V4.6.18i | V4.6.12i | V4.6.6i |
| *nn2 symmetry mutations of omnitruncated tilings: 4.2n.2n | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Symmetry *nn2 [n,n] |
Spherical | Euclidean | Compact hyperbolic | Paracomp. | ||||||||||
| *222 [2,2] |
*332 [3,3] |
*442 [4,4] |
*552 [5,5] |
*662 [6,6] |
*772 [7,7] |
*882 [8,8]... |
*∞∞2 [∞,∞] | |||||||
| Figure |  |
 |
 |
 |
 |
 |
 |
 | ||||||
| Config. | 4.4.4 | 4.6.6 | 4.8.8 | 4.10.10 | 4.12.12 | 4.14.14 | 4.16.16 | 4.∞.∞ | ||||||
| Dual |  |
 |
 |
 |
 |
 |
 |
 | ||||||
| Config. | V4.4.4 | V4.6.6 | V4.8.8 | V4.10.10 | V4.12.12 | V4.14.14 | V4.16.16 | V4.∞.∞ | ||||||
This polyhedron is a member of a sequence of uniform patterns with vertex figure (4.6.2p) and Coxeter-Dynkin diagram ![]()
![]()
![]()
![]()
![]() . For p < 6, the members of the sequence are omnitruncated polyhedra (zonohedra), shown below as spherical tilings. For p > 6, they are tilings of the hyperbolic plane, starting with the truncated triheptagonal tiling.
. For p < 6, the members of the sequence are omnitruncated polyhedra (zonohedra), shown below as spherical tilings. For p > 6, they are tilings of the hyperbolic plane, starting with the truncated triheptagonal tiling.
The truncated octahedron is topologically related as a part of sequence of uniform polyhedra and tilings with vertex figures n.6.6, extending into the hyperbolic plane:
| *n32 symmetry mutation of truncated tilings: n.6.6 | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Sym. *n42 [n,3] |
Spherical | Euclid. | Compact | Parac. | Noncompact hyperbolic | |||||||
| *232 [2,3] |
*332 [3,3] |
*432 [4,3] |
*532 [5,3] |
*632 [6,3] |
*732 [7,3] |
*832 [8,3]... |
*∞32 [∞,3] |
[12i,3] | [9i,3] | [6i,3] | ||
| Truncated figures |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 | |
| Config. | 2.6.6 | 3.6.6 | 4.6.6 | 5.6.6 | 6.6.6 | 7.6.6 | 8.6.6 | ∞.6.6 | 12i.6.6 | 9i.6.6 | 6i.6.6 | |
| n-kis figures |
 |
 |
 |
 |
 |
 |
 |
|||||
| Config. | V2.6.6 | V3.6.6 | V4.6.6 | V5.6.6 | V6.6.6 | V7.6.6 | V8.6.6 | V∞.6.6 | V12i.6.6 | V9i.6.6 | V6i.6.6 | |
The truncated octahedron is topologically related as a part of sequence of uniform polyhedra and tilings with vertex figures 4.2n.2n, extending into the hyperbolic plane:
| *n42 symmetry mutation of truncated tilings: 4.2n.2n | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Symmetry *n42 [n,4] |
Spherical | Euclidean | Compact hyperbolic | Paracomp. | |||||||
| *242 [2,4] |
*342 [3,4] |
*442 [4,4] |
*542 [5,4] |
*642 [6,4] |
*742 [7,4] |
*842 [8,4]... |
*∞42 [∞,4] | ||||
| Truncated figures |
 |
 |
 |
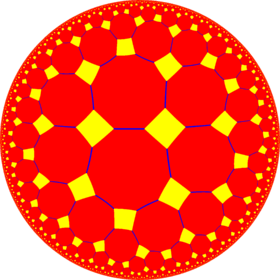 |
 |
 |
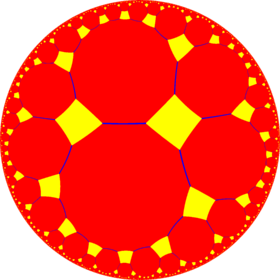 |
 | |||
| Config. | 4.4.4 | 4.6.6 | 4.8.8 | 4.10.10 | 4.12.12 | 4.14.14 | 4.16.16 | 4.∞.∞ | |||
| n-kis figures |
 |
 |
 |
 |
 |
 |
 |
 | |||
| Config. | V4.4.4 | V4.6.6 | V4.8.8 | V4.10.10 | V4.12.12 | V4.14.14 | V4.16.16 | V4.∞.∞ | |||
Related polytopes
The truncated octahedron (bitruncated cube), is first in a sequence of bitruncated hypercubes:
  |
  |
  |
 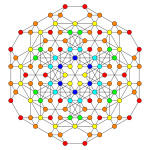 |
  |
  |
... |
| Bitruncated cube | Bitruncated tesseract | Bitruncated 5-cube | Bitruncated 6-cube | Bitruncated 7-cube | Bitruncated 8-cube | |
Tessellations
The truncated octahedron exists in three different convex uniform honeycombs (space-filling tessellations):
| Bitruncated cubic | Cantitruncated cubic | Truncated alternated cubic |
|---|---|---|
 |
 |
 |
The cell-transitive bitruncated cubic honeycomb can also be seen as the Voronoi tessellation of the body-centered cubic lattice. The truncated octahedron is one of five three-dimensional primary parallelohedra.
Truncated octahedral graph
| Truncated octahedral graph | |
|---|---|
|
3-fold symmetric schlegel diagram | |
| Vertices | 24 |
| Edges | 36 |
| Automorphisms | 48 |
| Chromatic number | 2 |
| Properties | Cubic, Hamiltonian, regular, zero-symmetric |
In the mathematical field of graph theory, a truncated octahedral graph is the graph of vertices and edges of the truncated octahedron, one of the Archimedean solids. It has 24 vertices and 36 edges, and is a cubic Archimedean graph.[2]
As a Hamiltonian cubic graph, it can be represented by LCF notation in multiple ways: [3, −7, 7, −3]6, [5, −11, 11, 7, 5, −5, −7, −11, 11, −5, −7, 7]2, and [−11, 5, −3, −7, −9, 3, −5, 5, −3, 9, 7, 3, −5, 11, −3, 7, 5, −7, −9, 9, 7, −5, −7, 3].[3]


References
- ↑ http://www.doskey.com/polyhedra/Stewart05.html
- ↑ Read, R. C.; Wilson, R. J. (1998), An Atlas of Graphs, Oxford University Press, p. 269
- ↑ Weisstein, Eric W. "Truncated octahedral graph". MathWorld.
- Williams, Robert (1979). The Geometrical Foundation of Natural Structure: A Source Book of Design. Dover Publications, Inc. ISBN 0-486-23729-X. (Section 3–9)
- Freitas, Robert A., Jr. "Uniform space-filling using only truncated octahedra". Figure 5.5 of Nanomedicine, Volume I: Basic Capabilities, Landes Bioscience, Georgetown, TX, 1999. Retrieved 2006-09-08. External link in
|publisher=(help) - Gaiha, P. & Guha, S.K. (1977). "Adjacent vertices on a permutohedron". SIAM Journal on Applied Mathematics. 32 (2): 323–327. doi:10.1137/0132025.
- Hart, George W. "VRML model of truncated octahedron". Virtual Polyhedra: The Encyclopedia of Polyhedra. Retrieved 2006-09-08. External link in
|publisher=(help) - Mäder, Roman. "The Uniform Polyhedra: Truncated Octahedron". Retrieved 2006-09-08.
- Alexandrov, A.D. (1958). Convex polyhedra. Berlin: Springer. p. 539. ISBN 3-540-23158-7.
- Cromwell, P. (1997). Polyhedra. United Kingdom: Cambridge. pp. 79–86 Archimedean solids. ISBN 0-521-55432-2.
External links
| Wikimedia Commons has media related to Truncated octahedron. |
- Template:Nowrapworld2
- Template:Nowrapworld
- Klitzing, Richard. "3D convex uniform polyhedra x3x4o - toe".
- Editable printable net of a truncated octahedron with interactive 3D view