Henri Lebesgue
| Henri Lebesgue | |
|---|---|
 | |
| Born |
June 28, 1875 Beauvais, Oise, France |
| Died |
July 26, 1941 (aged 66) Paris, France |
| Nationality | French |
| Fields | Mathematics |
| Institutions |
University of Rennes University of Poitiers University of Paris Collège de France |
| Alma mater |
École Normale Supérieure University of Paris |
| Doctoral advisor | Émile Borel |
| Doctoral students |
Paul Montel Zygmunt Janiszewski Georges de Rham |
| Known for |
Lebesgue integration Lebesgue measure |
| Notable awards |
Fellow of the Royal Society[1] Poncelet Prize for 1914[2] |
Henri Léon Lebesgue ForMemRS[1] (French: [ɑ̃ʁi leɔ̃ ləbɛɡ]; June 28, 1875 – July 26, 1941) was a French mathematician most famous for his theory of integration, which was a generalization of the 17th century concept of integration—summing the area between an axis and the curve of a function defined for that axis. His theory was published originally in his dissertation Intégrale, longueur, aire ("Integral, length, area") at the University of Nancy during 1902.[3][4]
Personal life
Henri Lebesgue was born on 28 June 1875 in Beauvais, Oise. Lebesgue's father was a typesetter and his mother was a school teacher. His parents assembled at home a library that the young Henri was able to use. His father died of tuberculosis when Lebesgue was still very young and his mother had to support him by herself. As he showed a remarkable talent for mathematics in primary school, one of his instructors arranged for community support to continue his education at the Collège de Beauvais and then at Lycée Saint-Louis and Lycée Louis-le-Grand in Paris.[5]
In 1894 Lebesgue was accepted at the École Normale Supérieure, where he continued to focus his energy on the study of mathematics, graduating in 1897. After graduation he remained at the École Normale Supérieure for two years, working in the library, where he became aware of the research on discontinuity done at that time by René-Louis Baire, a recent graduate of the school. At the same time he started his graduate studies at the Sorbonne, where he learned about Émile Borel's work on the incipient measure theory and Camille Jordan's work on the Jordan measure. In 1899 he moved to a teaching position at the Lycée Central in Nancy, while continuing work on his doctorate. In 1902 he earned his Ph.D. from the Sorbonne with the seminal thesis on "Integral, Length, Area", submitted with Borel, four years older, as advisor.[6]
Lebesgue married the sister of one of his fellow students, and he and his wife had two children, Suzanne and Jacques.
After publishing his thesis, Lebesgue was offered in 1902 a position at the University of Rennes, lecturing there until 1906, when he moved to the Faculty of Sciences of the University of Poitiers. In 1910 Lebesgue moved to the Sorbonne as a maître de conférences, being promoted to professor starting with 1919. In 1921 he left the Sorbonne to become professor of mathematics at the Collège de France, where he lectured and did research for the rest of his life.[7] In 1922 he was elected a member of the Académie des Sciences. Henri Lebesgue died on 26 July 1941 in Paris.[6]
Mathematical career

Lebesgue's first paper was published in 1898 and was titled "Sur l'approximation des fonctions". It dealt with Weierstrass' theorem on approximation to continuous functions by polynomials. Between March 1899 and April 1901 Lebesgue published six notes in Comptes Rendus. The first of these, unrelated to his development of Lebesgue integration, dealt with the extension of Baire's theorem to functions of two variables. The next five dealt with surfaces applicable to a plane, the area of skew polygons, surface integrals of minimum area with a given bound, and the final note gave the definition of Lebesgue integration for some function f(x). Lebesgue's great thesis, Intégrale, longueur, aire, with the full account of this work, appeared in the Annali di Matematica in 1902. The first chapter develops the theory of measure (see Borel measure). In the second chapter he defines the integral both geometrically and analytically. The next chapters expand the Comptes Rendus notes dealing with length, area and applicable surfaces. The final chapter deals mainly with Plateau's problem. This dissertation is considered to be one of the finest ever written by a mathematician.[1]
His lectures from 1902 to 1903 were collected into a "Borel tract" Leçons sur l'intégration et la recherche des fonctions primitives. The problem of integration regarded as the search for a primitive function is the keynote of the book. Lebesgue presents the problem of integration in its historical context, addressing Augustin-Louis Cauchy, Peter Gustav Lejeune Dirichlet, and Bernhard Riemann. Lebesgue presents six conditions which it is desirable that the integral should satisfy, the last of which is "If the sequence fn(x) increases to the limit f(x), the integral of fn(x) tends to the integral of f(x)." Lebesgue shows that his conditions lead to the theory of measure and measurable functions and the analytical and geometrical definitions of the integral.
He turned next to trigonometric functions with his 1903 paper "Sur les séries trigonométriques". He presented three major theorems in this work: that a trigonometrical series representing a bounded function is a Fourier series, that the nth Fourier coefficient tends to zero (the Riemann–Lebesgue lemma), and that a Fourier series is integrable term by term. In 1904-1905 Lebesgue lectured once again at the Collège de France, this time on trigonometrical series and he went on to publish his lectures in another of the "Borel tracts". In this tract he once again treats the subject in its historical context. He expounds on Fourier series, Cantor-Riemann theory, the Poisson integral and the Dirichlet problem.
In a 1910 paper, "Représentation trigonométrique approchée des fonctions satisfaisant a une condition de Lipschitz" deals with the Fourier series of functions satisfying a Lipschitz condition, with an evaluation of the order of magnitude of the remainder term. He also proves that the Riemann–Lebesgue lemma is a best possible result for continuous functions, and gives some treatment to Lebesgue constants.
Lebesgue once wrote, "Réduites à des théories générales, les mathématiques seraient une belle forme sans contenu." ("Reduced to general theories, mathematics would be a beautiful form without content.")
In measure-theoretic analysis and related branches of mathematics, the Lebesgue–Stieltjes integral generalizes Riemann–Stieltjes and Lebesgue integration, preserving the many advantages of the latter in a more general measure-theoretic framework.
During the course of his career, Lebesgue also made forays into the realms of complex analysis and topology. He also had a disagreement with Borel with regards to effective calculation. However, these minor forays pale in comparison to his contributions to real analysis; his contributions to this field had a tremendous impact on the shape of the field today and his methods have become an essential part of modern analysis.
Lebesgue's theory of integration
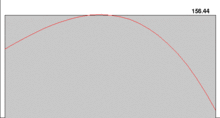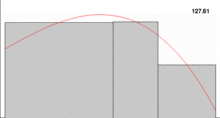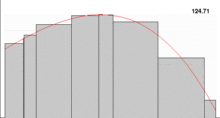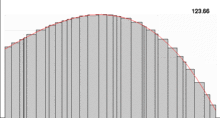
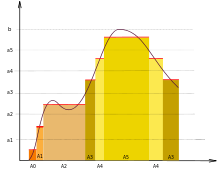
- This is a non-technical treatment from a historical point of view; see the article Lebesgue integration for a technical treatment from a mathematical point of view.
Integration is a mathematical operation that corresponds to the informal idea of finding the area under the graph of a function. The first theory of integration was developed by Archimedes in the 3rd century BC with his method of quadratures, but this could be applied only in limited circumstances with a high degree of geometric symmetry. In the 17th century, Isaac Newton and Gottfried Wilhelm Leibniz discovered the idea that integration was intrinsically linked to differentiation, the latter being a way of measuring how quickly a function changed at any given point on the graph. This surprising relationship between two major geometric operations in calculus, differentiation and integration, is now known as the Fundamental Theorem of Calculus. It has allowed mathematicians to calculate a broad class of integrals for the first time. However, unlike Archimedes' method, which was based on Euclidean geometry, mathematicians felt that Newton's and Leibniz's integral calculus did not have a rigorous foundation.
In the 19th century, Augustin Cauchy developed epsilon-delta limits, and Bernhard Riemann followed up on this by formalizing what is now called the Riemann integral. To define this integral, one fills the area under the graph with smaller and smaller rectangles and takes the limit of the sums of the areas of the rectangles at each stage. For some functions, however, the total area of these rectangles does not approach a single number. As such, they have no Riemann integral.
Lebesgue invented a new method of integration to solve this problem. Instead of using the areas of rectangles, which put the focus on the domain of the function, Lebesgue looked at the codomain of the function for his fundamental unit of area. Lebesgue's idea was to first define measure, for both sets and functions on those sets. He then proceeded to build the integral for what he called simple functions; measurable functions that take only finitely many values. Then he defined it for more complicated functions as the least upper bound of all the integrals of simple functions smaller than the function in question.
Lebesgue integration has the property that every function defined over a bounded interval with a Riemann integral also has a Lebesgue integral, and for those functions the two integrals agree. Furthermore, every bounded function on a closed bounded interval has a Lebesgue integral and there are many functions with a Lebesgue integral that have no Riemann integral.
As part of the development of Lebesgue integration, Lebesgue invented the concept of measure, which extends the idea of length from intervals to a very large class of sets, called measurable sets (so, more precisely, simple functions are functions that take a finite number of values, and each value is taken on a measurable set). Lebesgue's technique for turning a measure into an integral generalises easily to many other situations, leading to the modern field of measure theory.
The Lebesgue integral is deficient in one respect. The Riemann integral generalises to the improper Riemann integral to measure functions whose domain of definition is not a closed interval. The Lebesgue integral integrates many of these functions (always reproducing the same answer when it did), but not all of them. For functions on the real line, the Henstock integral is an even more general notion of integral (based on Riemann's theory rather than Lebesgue's) that subsumes both Lebesgue integration and improper Riemann integration. However, the Henstock integral depends on specific ordering features of the real line and so does not generalise to allow integration in more general spaces (say, manifolds), while the Lebesgue integral extends to such spaces quite naturally.
See also
- Dominated convergence theorem
- Lebesgue covering dimension
- Lebesgue point
- Lebesgue's number lemma
- Lebesgue spine
- Lebesgue constant (interpolation)
References
- 1 2 3 Burkill, J. C. (1944). "Henri Lebesgue. 1875-1941". Obituary Notices of Fellows of the Royal Society. 4 (13): 483. doi:10.1098/rsbm.1944.0001. JSTOR 768841.
- ↑ "Prizes Awarded by the Paris Academy of Sciences for 1914". Nature. 94 (2358): 518–519. 7 January 1915. doi:10.1038/094518a0.
- ↑ Henri Lebesgue at the Mathematics Genealogy Project
- ↑ O'Connor, John J.; Robertson, Edmund F., "Henri Lebesgue", MacTutor History of Mathematics archive, University of St Andrews.
- ↑ Hawking, Stephen W. (2005). God created the integers: the mathematical breakthroughs that changed history. Running Press. pp. 1041–87. ISBN 978-0-7624-1922-7.
- 1 2 McElroy, Tucker (2005). A to Z of mathematicians. Infobase Publishing. p. 164. ISBN 978-0-8160-5338-4.
- ↑ Perrin, Louis (2004). "Henri Lebesgue: Renewer of Modern Analysis". In Le Lionnais, François. Great Currents of Mathematical Thought. 1 (2nd ed.). Courier Dover Publications. ISBN 978-0-486-49578-1.