Overfitting

The green line represents an overfitted model and the black line represents a regularised model. While the green line best follows the training data, it is too dependent on it and it is likely to have a higher error rate on new unseen data, compared to the black line.

Noisy (roughly linear) data is fitted to both linear and polynomial functions. Although the polynomial function is a perfect fit, the linear version can be expected to generalize better. In other words, if the two functions were used to extrapolate the data beyond the fit data, the linear function would make better predictions.

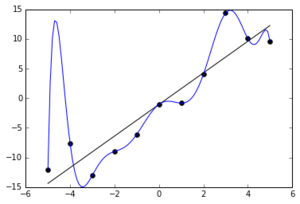
In statistics and machine learning, one of the most common tasks is to fit a "model" to a set of training data, so as to be able to make reliable predictions on general untrained data. In overfitting, a statistical model describes random error or noise instead of the underlying relationship. Overfitting occurs when a model is excessively complex, such as having too many parameters relative to the number of observations. A model that has been overfit has poor predictive performance, as it overreacts to minor fluctuations in the training data.

The possibility of overfitting exists because the criterion used for training the model is not the same as the criterion used to judge the efficacy of a model. In particular, a model is typically trained by maximizing its performance on some set of training data. However, its efficacy is determined not by its performance on the training data but by its ability to perform well on unseen data. Overfitting occurs when a model begins to "memorize" training data rather than "learning" to generalize from trend. As an extreme example, if the number of parameters is the same as or greater than the number of observations, a simple model or learning process can perfectly predict the training data simply by memorizing the training data in its entirety, but such a model will typically fail drastically when making predictions about new or unseen data, since the simple model has not learned to generalize at all.

The potential for overfitting depends not only on the number of parameters and data but also the conformability of the model structure with the data shape, and the magnitude of model error compared to the expected level of noise or error in the data.

Even when the fitted model does not have an excessive number of parameters, it is to be expected that the fitted relationship will appear to perform less well on a new data set than on the data set used for fitting.^[1] In particular, the value of the coefficient of determination will shrink relative to the original training data.

In order to avoid overfitting, it is necessary to use additional techniques (e.g. cross-validation, regularization, early stopping, pruning, Bayesian priors on parameters or model comparison), that can indicate when further training is not resulting in better generalization. The basis of some techniques is either (1) to explicitly penalize overly complex models, or (2) to test the model's ability to generalize by evaluating its performance on a set of data not used for training, which is assumed to approximate the typical unseen data that a model will encounter.

A good analogy for the overfitting problem is imagine a baby trying to learn what is a window or what is not a window, we start to show him windows and he detects at a initial phase that all windows have glasses, and a frame and you can look outside, some of them may be opened. If we keep showing the same windows the baby may also falsely deduce that all windows are green, and that all green frames are windows. Thus overfitting the problem.

Machine learning

Overfitting/overtraining in supervised learning (e.g., neural network). Training error is shown in blue, validation error in red, both as a function of the number of training cycles. If the validation error increases(positive slope) while the training error steadily decreases(negative slope) then a situation of overfitting may have occurred. The best predictive and fitted model would be where the validation error has its global minimum.

Usually a learning algorithm is trained using some set of "training data": exemplary situations for which the desired output is known. The goal is that the algorithm will also perform well on predicting the output when fed "validation data" that was not encountered during its training.

Overfitting is the use of models or procedures that violate Occam's razor, for example by including more adjustable parameters than are ultimately optimal, or by using a more complicated approach than is ultimately optimal. For an example where there are too many adjustable parameters, consider a dataset where training data for $y$ can be adequately predicted by a linear function of two dependent variables. Such a function requires only three parameters (the intercept and two slopes). Replacing this simple function with a new, more complex quadratic function, or with a new, more complex linear function on more than two dependent variables, carries a risk: Occam's razor implies that any given complex function is a priori less probable than any given simple function. If the new, more complicated function is selected instead of the simple function, and if there was not a large enough gain in training-data fit to offset the complexity increase, then the new complex function "overfits" the data, and the complex overfitted function will likely perform worse than the simpler function on validation data outside the training dataset, even though the complex function performed as well, or perhaps even better, on the training dataset.^[2]

When comparing different types of models, complexity cannot be measured solely by counting how many parameters exist in each model; the expressivity of each parameter must be considered as well. For example, it is nontrivial to directly compare the complexity of a neural net (which can track curvilinear relationships) with $m$ parameters to a regression model with $n$ parameters.^[2]

Overfitting is especially likely in cases where learning was performed too long or where training examples are rare, causing the learner to adjust to very specific random features of the training data, that have no causal relation to the target function. In this process of overfitting, the performance on the training examples still increases while the performance on unseen data becomes worse.

As a simple example, consider a database of retail purchases that includes the item bought, the purchaser, and the date and time of purchase. It's easy to construct a model that will fit the training set perfectly by using the date and time of purchase to predict the other attributes; but this model will not generalize at all to new data, because those past times will never occur again.

Generally, a learning algorithm is said to overfit relative to a simpler one if it is more accurate in fitting known data (hindsight) but less accurate in predicting new data (foresight). One can intuitively understand overfitting from the fact that information from all past experience can be divided into two groups: information that is relevant for the future and irrelevant information ("noise"). Everything else being equal, the more difficult a criterion is to predict (i.e., the higher its uncertainty), the more noise exists in past information that needs to be ignored. The problem is determining which part to ignore. A learning algorithm that can reduce the chance of fitting noise is called robust.

Consequences

The most obvious consequence of overfitting is poor performance on the validation dataset. Other negative consequences include:^[2]

A function that is overfitted is likely to request more information about each item in the validation dataset than does the optimal function; gathering this additional unneeded data can be expensive or error-prone, especially if each individual piece of information must be gathered by human observation and manual data-entry.
A more complex, overfitted function is likely to be less portable than a simple one. At one extreme, a one-variable linear regression is so portable that, if necessary, it could even be done by hand. At the other extreme are models that can be reproduced only by exactly duplicating the original modeler's entire setup, making reuse or scientific reproduction difficult.

Regression

Outside machine learning, overfitting is also a problem in the broad study of regression, including regression done "by hand". In the extreme case, if there are p variables in a linear regression with p data points, the fitted line will go exactly through every point. ^[3] There is a variety of rules of thumb for the number of observations needed per independent variable, including 10 ^[4] and 10-15.^[5]

References

↑ Everitt B.S. (2002) Cambridge Dictionary of Statistics, CUP. ISBN 0-521-81099-X (entry for "Shrinkage")
1 2 3 Hawkins, Douglas M. "The problem of overfitting." Journal of chemical information and computer sciences 44.1 (2004): 1-12.
↑ Martha K. Smith (2014-06-13). "Overfitting". University of Texas at Austin. Retrieved 2016-07-31.
↑ Draper, Norman R.; Smith, Harry (1998). Applied regression analysis, 3rd Edition. New York: Wiley. ISBN 978-0471170822.
↑ Jim Frost (2015-09-03). "The Danger of Overfitting Regression Models". Retrieved 2016-07-31.

Leinweber, D. J. (2007). "Stupid Data Miner Tricks". The Journal of Investing. 16: 15–22. doi:10.3905/joi.2007.681820.

Tetko, I. V.; Livingstone, D. J.; Luik, A. I. (1995). "Neural network studies. 1. Comparison of Overfitting and Overtraining" (PDF). J. Chem. Inf. Comput. Sci. 35 (5): 826–833. doi:10.1021/ci00027a006.

External links

Overfitting: when accuracy measure goes wrong - an introductory video tutorial.
The Problem of Overfitting Data
CSE546: Linear Regression Bias / Variance Tradeoff

This article is issued from Wikipedia - version of the 11/13/2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.