Symbolic power of a prime ideal

In algebra, given a ring R and a prime ideal P in it, the n-th symbolic power of P is the ideal

P^{(n)} = P^n R_P \cap R = \{ f \in R \mid sf \in P^n \text{ for some }s \in R - P \}.

^[1]

It is the smallest P-primary ideal containing the n-th power Pⁿ. Very roughly, it consists of functions with zeros of order n along the variety defined by P. If R is Noetherian, then it is the P-primary component in the primary decomposition of Pⁿ. We have: 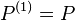$P^{(1)} = P$ and if P is a maximal ideal, then $P^{(n)} = P^n$ .

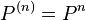References

↑ Here, by abuse of notation, we write $I \cap R$ to mean the pre-image of I along the localization map $R \to R_P$ .

http://www.math.lsa.umich.edu/~hochster/711F07/L09.07.pdf

This article is issued from Wikipedia - version of the 9/16/2014. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.