Residue-class-wise affine group
In mathematics, specifically in group theory, residue-class-wise affine
groups are certain permutation groups acting on
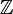 (the integers), whose elements are bijective
residue-class-wise affine mappings.
(the integers), whose elements are bijective
residue-class-wise affine mappings.
A mapping 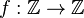 is called residue-class-wise affine
if there is a nonzero integer
is called residue-class-wise affine
if there is a nonzero integer 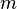 such that the restrictions of
such that the restrictions of  to the residue classes
(mod
to the residue classes
(mod 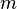 ) are all affine. This means that for any
residue class
) are all affine. This means that for any
residue class 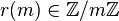 there are coefficients
there are coefficients
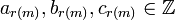 such that the restriction of the mapping
such that the restriction of the mapping  to the set
to the set 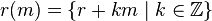 is given by
is given by
 .
.
Residue-class-wise affine groups are countable, and they are accessible
to computational investigations.
Many of them act multiply transitively on 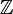 or on subsets thereof.
or on subsets thereof.
A particularly basic type of residue-class-wise affine permutations are the
class transpositions: given disjoint residue classes 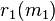 and
and 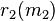 , the corresponding class transposition is the permutation
of
, the corresponding class transposition is the permutation
of 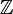 which interchanges
which interchanges  and
and
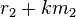 for every
for every 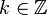 and which
fixes everything else. Here it is assumed that
and which
fixes everything else. Here it is assumed that
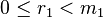 and that
and that  .
.
The set of all class transpositions of 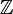 generates
a countable simple group which has the following properties:
generates
a countable simple group which has the following properties:
- It is not finitely generated.
- Every finite group, every free product of finite groups and every free group of finite rank embeds into it.
- The class of its subgroups is closed under taking direct products, under taking wreath products with finite groups, and under taking restricted wreath products with the infinite cyclic group.
- It has finitely generated subgroups which do not have finite presentations.
- It has finitely generated subgroups with algorithmically unsolvable membership problem.
- It has an uncountable series of simple subgroups which is parametrized by the sets of odd primes.
It is straightforward to generalize the notion of a residue-class-wise affine group
to groups acting on suitable rings other than 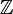 ,
though only little work in this direction has been done so far.
,
though only little work in this direction has been done so far.
See also the Collatz conjecture, which is an assertion about a surjective, but not injective residue-class-wise affine mapping.
References and external links
- Stefan Kohl. Restklassenweise affine Gruppen. Dissertation, Universität Stuttgart, 2005. Archivserver der Deutschen Nationalbibliothek OPUS-Datenbank(Universität Stuttgart)
- Stefan Kohl. RCWA – Residue-Class-Wise Affine Groups. GAP package. 2005.
- Stefan Kohl. A Simple Group Generated by Involutions Interchanging Residue Classes of the Integers. Math. Z. 264 (2010), no. 4, 927–938.