Relative key



In music, relative keys are the major and minor scales that have the same key signatures. A pair of major and minor scales sharing the same key signature are said to be in a relative relationship.[1] The relative minor of a particular major key, or the relative major of a minor key, is the key which has the same key signature but a different tonic; this is as opposed to parallel minor or major, which shares the same tonic. Relative keys are closely related keys, the keys between which most modulations occur, in that they differ by no more than one accidental (none in the case of relative keys).[2]
The minor key starts three semitones below its relative major; for example, A minor is three semitones below its relative, C Major.
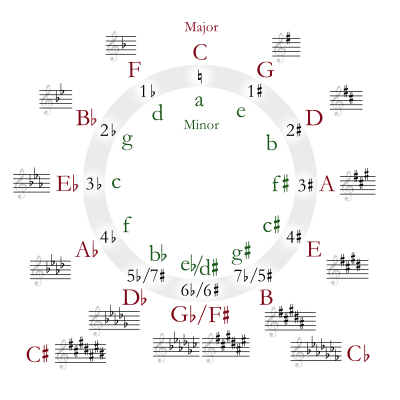
G major and E minor both have a single sharp in their key signature at F♯; therefore, E minor is the relative minor of G major, and conversely G major is the relative major of E minor. The tonic of the relative minor is the sixth scale degree of the major scale, while the tonic of the relative major is the third degree of the minor scale.[1] The relative relationship may be visualized through the circle of fifths.[1]
A complete list of relative minor/major pairs in order of the circle of fifths is:
| Key signature | Major key | Minor key |
|---|---|---|
| B♭, E♭, A♭, D♭, G♭, C♭, F♭ | C♭ major | A♭ minor |
| B♭, E♭, A♭, D♭, G♭, C♭ | G♭ major | E♭ minor |
| B♭, E♭, A♭, D♭, G♭ | D♭ major | B♭ minor |
| B♭, E♭, A♭, D♭ | A♭ major | F minor |
| B♭, E♭, A♭ | E♭ major | C minor |
| B♭, E♭ | B♭ major | G minor |
| B♭ | F major | D minor |
| C major | A minor | |
| F♯ | G major | E minor |
| F♯, C♯ | D major | B minor |
| F♯, C♯, G♯ | A major | F♯ minor |
| F♯, C♯, G♯, D♯ | E major | C♯ minor |
| F♯, C♯, G♯, D♯, A♯ | B major | G♯ minor |
| F♯, C♯, G♯, D♯, A♯, E♯ | F♯ major | D♯ minor |
| F♯, C♯, G♯, D♯, A♯, E♯, B♯ | C♯ major | A♯ minor |
Terminology
Confusingly, the term for "relative key" in German is paralleltonart, while parallel key is varianttonart. Similar terminology is used in most Germanic and Slavic languages, but not Romance languages. This is in particular confusing with the term parallel chord, which denotes chords derived from the relative key in English usage.