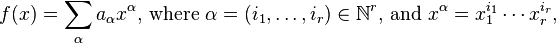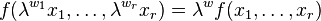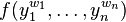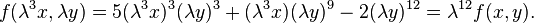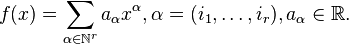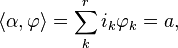Quasi-homogeneous polynomial
In algebra, a multivariate polynomial
is quasi-homogeneous or weighted homogeneous, if there exists r integers  , called weights of the variables, such that the sum
, called weights of the variables, such that the sum  is the same for all nonzero terms of f. This sum w is the weight or the degree of the polynomial.
is the same for all nonzero terms of f. This sum w is the weight or the degree of the polynomial.
The term quasi-homogeneous comes form the fact that a polynomial f is quasi-homogeneous if and only if
for every 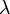 in any field containing the coefficients.
in any field containing the coefficients.
A polynomial  is quasi-homogeneous with weights
is quasi-homogeneous with weights  if and only if
if and only if
is a homogeneous polynomial in the 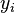 . In particular, a homogeneous polynomial is always quasi-homogeneous, with all weights equal to 1.
. In particular, a homogeneous polynomial is always quasi-homogeneous, with all weights equal to 1.
In other words, a polynomial is quasi-homogeneous if all the  belong to the same affine hyperplane. As the Newton polygon of the polynomial is the convex hull of the set
belong to the same affine hyperplane. As the Newton polygon of the polynomial is the convex hull of the set 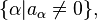 the quasi-homogeneous polynomials may also be defined as the polynomials that have a degenerate Newton polynomial (here "degenerate" means "contained in some affine hyperplane").
the quasi-homogeneous polynomials may also be defined as the polynomials that have a degenerate Newton polynomial (here "degenerate" means "contained in some affine hyperplane").
Introduction
Consider the polynomial 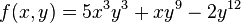 . This one has no chance of being a homogeneous polynomial; however if instead of considering
. This one has no chance of being a homogeneous polynomial; however if instead of considering  we use the pair
we use the pair  to test homogeneity, then
to test homogeneity, then
We say that 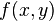 is a quasi-homogeneous polynomial of type
(3,1), because its three pairs (i1,i2) of exponents (3,3), (1,9) and (0,12) all satisfy the linear equation
is a quasi-homogeneous polynomial of type
(3,1), because its three pairs (i1,i2) of exponents (3,3), (1,9) and (0,12) all satisfy the linear equation  . In particular, this says that the Newton polygon of
. In particular, this says that the Newton polygon of 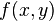 lies in the affine space with equation
lies in the affine space with equation 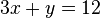 inside
inside  .
.
The above equation is equivalent to this new one:  . Some authors[1] prefer to use this last condition and prefer to say that our polynomial is quasi-homogeneous of type (
. Some authors[1] prefer to use this last condition and prefer to say that our polynomial is quasi-homogeneous of type ( ).
).
As noted above, a homogeneous polynomial 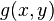 of degree d is just a quasi-homogeneous polynomial of type (1,1); in this case all its pairs of exponents will satisfy the equation
of degree d is just a quasi-homogeneous polynomial of type (1,1); in this case all its pairs of exponents will satisfy the equation  .
.
Definition
Let 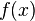 be a polynomial in r variables
be a polynomial in r variables 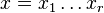 with coefficients in a commutative ring R. We express it as a finite sum
with coefficients in a commutative ring R. We express it as a finite sum
We say that f is quasi-homogeneous of type 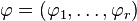 ,
,  if there exists some
if there exists some 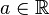 such that
such that
whenever  .
.
References
- ↑ J. Steenbrink (1977). Compositio Mathematica, tome 34, n° 2. Noordhoff International Publishing. p. 211 (Available on-line at Numdam)