Quadric
In mathematics, a quadric or quadric surface (quadric hypersurface if D > 2), is a generalization of conic sections (ellipses, parabolas, and hyperbolas) to any number of dimensions. It is any D-dimensional hypersurface in (D + 1)-dimensional space defined as the locus of zeros of a quadratic polynomial (D=1 in the case of conic sections). In coordinates x1, x2, ..., xD+1, the general quadric is defined by the algebraic equation[1]
which may be compactly written in vector and matrix notation as:
where x = (x1, x2, ..., xD+1) is a row vector, xT is the transpose of x (a column vector), Q is a (D + 1) × (D + 1) matrix and P is a (D + 1)-dimensional row vector and R a scalar constant. The values Q, P and R are often taken to be over real numbers or complex numbers, but a quadric may be defined over any ring.
In general, the locus of zeros of a set of polynomials is known as an algebraic set, and is studied in the branch of algebraic geometry. A quadric is thus an example of an algebraic set. For the projective theory see Quadric (projective geometry).
Euclidean plane
Quadrics in the Euclidean plane are those of dimension D = 1, which is to say that they are curves. Such quadrics are the same as conic sections, and are typically known as conics rather than quadrics.

Euclidean space
In Euclidean space, quadrics have dimension D = 2, and are known as quadric surfaces. By making a suitable Euclidean change of variables, any quadric in Euclidean space can be put into a certain normal form by choosing as the coordinate directions the principal axes of the quadric. In three-dimensional Euclidean space there are 16 such normal forms.[2] Of these 16 forms, five are nondegenerate, and the remaining are degenerate forms. Degenerate forms include planes, lines, points or even no points at all.[3]
| Non-degenerate real quadric surfaces | ||
|---|---|---|
| Ellipsoid | 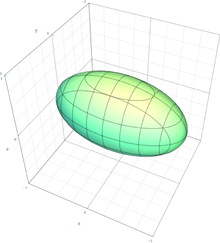 | |
| Spheroid (special case of ellipsoid) |   | |
| Sphere (special case of spheroid) |  | |
| Elliptic paraboloid | ||
| Circular paraboloid (special case of elliptic paraboloid) |  | |
| Hyperbolic paraboloid |  | |
| Elliptic hyperboloid of one sheet |  | |
| Circular hyperboloid of one sheet (special case of elliptic hyperboloid of one sheet) | 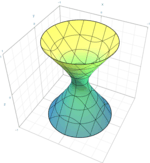 | |
| Elliptic hyperboloid of two sheets |  | |
| Circular hyperboloid of two sheets (special case of elliptic hyperboloid of two sheets) |  | |
| Degenerate quadric surfaces | ||
| Elliptic cone | ||
| Circular cone (special case of cone) |  | |
| Elliptic cylinder |  | |
| Circular cylinder (special case of elliptic cylinder) |  | |
| Hyperbolic cylinder | 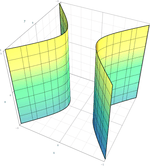 | |
| Parabolic cylinder |  | |
Projective geometry
The quadrics can be treated in a uniform manner by introducing homogeneous coordinates on a Euclidean space, thus effectively regarding it as a projective space. Thus if the original (affine) coordinates on RD+1 are
one introduces new coordinates on RD+2
related to the original coordinates by . In the new variables, every quadric is defined by an equation of the form
where the coefficients aij are symmetric in i and j. Regarding Q(X) = 0 as an equation in projective space exhibits the quadric as a projective algebraic variety. The quadric is said to be non-degenerate if the quadratic form is non-singular; equivalently, if the matrix (aij) is invertible.
In real projective space, by Sylvester's law of inertia, a non-singular quadratic form Q(X) may be put into the normal form
by means of a suitable projective transformation (normal forms for singular quadrics can have zeros as well as ±1 as coefficients). For surfaces in space (dimension D = 2) there are exactly three nondegenerate cases:
The first case is the empty set.
The second case generates the ellipsoid, the elliptic paraboloid or the hyperboloid of two sheets, depending on whether the chosen plane at infinity cuts the quadric in the empty set, in a point, or in a nondegenerate conic respectively. These all have positive Gaussian curvature.
The third case generates the hyperbolic paraboloid or the hyperboloid of one sheet, depending on whether the plane at infinity cuts it in two lines, or in a nondegenerate conic respectively. These are doubly ruled surfaces of negative Gaussian curvature.
The degenerate form
generates the elliptic cylinder, the parabolic cylinder, the hyperbolic cylinder, or the cone, depending on whether the plane at infinity cuts it in a point, a line, two lines, or a nondegenerate conic respectively. These are singly ruled surfaces of zero Gaussian curvature.
We see that projective transformations don't mix Gaussian curvatures of different sign. This is true for general surfaces. [4]
In complex projective space all of the nondegenerate quadrics become indistinguishable from each other.
See also
References
- ↑ Silvio Levy Quadrics in "Geometry Formulas and Facts", excerpted from 30th Edition of CRC Standard Mathematical Tables and Formulas, CRC Press, from The Geometry Center at University of Minnesota
- ↑ Sameen Ahmed Khan,Quadratic Surfaces in Science and Engineering, Bulletin of the IAPT, 2(11), 327–330 (November 2010). (Publication of the Indian Association of Physics Teachers).
Sameen Ahmed Khan, Coordinate Geometric Generalization of the Spherometer and Cylindrometer, arXiv:1311.3602 - ↑ Stewart Venit and Wayne Bishop, Elementary Linear Algebra (fourth edition), International Thompson Publishing, 1996.
- ↑ S. Lazebnik and J. Ponce, "The Local Projective Shape of Smooth Surfaces and Their Outlines" (PDF)., Proposition 1
- Iskovskikh, V.A. (2001), "Quadric", in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4
- Weisstein, Eric W. "Quadric". MathWorld.