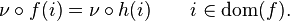Complete numbering
In computability theory complete numberings are generalizations of Gödel numbering first introduced by A.I. Mal'tsev in 1963. They are studied because several important results like the Kleene's recursion theorem and Rice's theorem, which were originally proven for the Gödel-numbered set of computable functions, still hold for arbitrary sets with complete numberings.
Definition
A numbering  of a set
of a set  is called complete (with respect to an element
is called complete (with respect to an element  ) if for every partial computable function
) if for every partial computable function  there exists a total computable function
there exists a total computable function 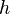 so that
so that
The numbering  is called precomplete if
is called precomplete if
Examples
- any numbering of a singleton set is complete
- the identity function on the natural numbers is not complete
- a Gödel numbering is precomplete
References
- A.I. Mal'tsev, Sets with complete numberings. Algebra i Logika, 1963, vol. 2, no. 2, 4-29 (Russian)
This article is issued from Wikipedia - version of the 12/2/2012. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.