Pointed space
In mathematics, a pointed space is a topological space with a distinguished point, the basepoint. The distinguished point is just simply one particular point, picked out from the space, and given a name, such as x0, that remains unchanged during subsequent discussion, and is kept track of during all operations.
Maps of pointed spaces (based maps) are continuous maps preserving basepoints, i.e., a map f between a pointed space X with basepoint x0 and a pointed space Y with basepoint y0 is a based map if it is continuous with respect to the topologies of X and Y and if f(x0) = y0. This is usually denoted
- f : (X, x0) → (Y, y0).
Pointed spaces are important in algebraic topology, particularly in homotopy theory, where many constructions, such as the fundamental group, depend on a choice of basepoint.
The pointed set concept is less important; it is anyway the case of a pointed discrete space.
Pointed spaces are often taken as a special case of the relative topology, where the subset is a single point. Thus, much of homotopy theory is usually developed on pointed spaces, and then moved to relative topologies in algebraic topology.
Category of pointed spaces
The class of all pointed spaces forms a category Top• with basepoint preserving continuous maps as morphisms. Another way to think about this category is as the comma category, ({•} ↓ Top) where {•} is any one point space and Top is the category of topological spaces. (This is also called a coslice category denoted {•}/Top.) Objects in this category are continuous maps {•} → X. Such morphisms can be thought of as picking out a basepoint in X. Morphisms in ({•} ↓ Top) are morphisms in Top for which the following diagram commutes:
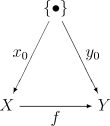
It is easy to see that commutativity of the diagram is equivalent to the condition that f preserves basepoints.
As a pointed space {•} is a zero object in Top• while it is only a terminal object in Top.
There is a forgetful functor Top• → Top which "forgets" which point is the basepoint. This functor has a left adjoint which assigns to each topological space X the disjoint union of X and a one-point space {•} whose single element is taken to be the basepoint.
Operations on pointed spaces
- A subspace of a pointed space X is a topological subspace A ⊆ X which shares its basepoint with X so that the inclusion map is basepoint preserving.
- One can form the quotient of a pointed space X under any equivalence relation. The basepoint of the quotient is the image of the basepoint in X under the quotient map.
- One can form the product of two pointed spaces (X, x0), (Y, y0) as the topological product X × Y with (x0, y0) serving as the basepoint.
- The coproduct in the category of pointed spaces is the wedge sum, which can be thought of as the one-point union of spaces.
- The smash product of two pointed spaces is essentially the quotient of the direct product and the wedge sum. We would like to say that the smash product turns the category of pointed spaces into a symmetric monoidal category with the pointed 0-sphere as the unit object, but this is false for general spaces: the associativity condition might fail. But it is true for some more restricted categories of spaces, such as compactly generated weak Hausdorff ones.
- The reduced suspension ΣX of a pointed space X is (up to a homeomorphism) the smash product of X and the pointed circle S1.
- The reduced suspension is a functor from the category of pointed spaces to itself. This functor is a left adjoint to the functor taking a based space to its loop space .
References
- Gamelin, Theodore W.; Greene, Robert Everist (1999) [1983]. Introduction to Topology (second ed.). Dover Publications. ISBN 0-486-40680-6.
- Mac Lane, Saunders (September 1998). Categories for the Working Mathematician (second ed.). Springer. ISBN 0-387-98403-8.