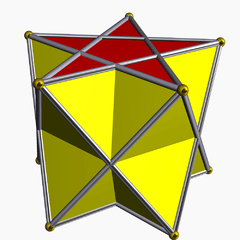
Pentagrammic antiprism
| Uniform Pentagrammic antiprism | |
|---|---|
 | |
| Type | Prismatic uniform polyhedron |
| Elements | F = 12, E = 20 V = 10 (χ = 2) |
| Faces by sides | 10{3}+2{5/2} |
| Schläfli symbol | sr{2,5/2} |
| Wythoff symbol | | 2 2 5/2 |
| Coxeter diagram | |
| Symmetry | D5h, [5,2], (*552), order 20 |
| Rotation group | D5, [5,2]+, (55), order 10 |
| Index references | U79(a) |
| Dual | Pentagrammic trapezohedron |
| Properties | nonconvex |
 Vertex figure 3.3.3.5/2 | |
In geometry, the pentagrammic antiprism is one in an infinite set of nonconvex antiprisms formed by triangle sides and two regular star polygon caps, in this case two pentagrams.
This polyhedron is identified with the indexed name U79 as a uniform polyhedron.

An alternative representation with hollow centers to the pentagrams.
Net
Net (fold the dotted line in the centre in the opposite direction to all the other lines):

See also
External links
- http://www.mathconsult.ch/showroom/unipoly/04.html
- http://www.math.technion.ac.il/~rl/kaleido/data/04.html
This article is issued from Wikipedia - version of the 12/10/2013. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.