Noetherian scheme
In algebraic geometry, a noetherian scheme is a scheme that admits a finite covering by open affine subsets 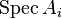 ,
, 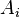 noetherian rings. More generally, a scheme is locally noetherian if it is covered by spectra of noetherian rings. Thus, a scheme is noetherian if and only if it is locally noetherian and quasi-compact. As with noetherian rings, the concept is named after Emmy Noether.
noetherian rings. More generally, a scheme is locally noetherian if it is covered by spectra of noetherian rings. Thus, a scheme is noetherian if and only if it is locally noetherian and quasi-compact. As with noetherian rings, the concept is named after Emmy Noether.
It can be shown that, in a locally noetherian scheme, if 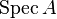 is an open affine subset, then A is a noetherian ring. In particular,
is an open affine subset, then A is a noetherian ring. In particular, 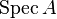 is a noetherian scheme if and only if A is a noetherian ring. Let X be a locally noetherian scheme. Then the local rings
is a noetherian scheme if and only if A is a noetherian ring. Let X be a locally noetherian scheme. Then the local rings 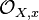 are noetherian rings.
are noetherian rings.
A noetherian scheme is a noetherian topological space. But the converse is false in general; consider, for example, the spectrum of a non-noetherian valuation ring.
The definitions extend to formal schemes.
References
- Robin Hartshorne, Algebraic geometry.