Matroid polytope
In mathematics, a matroid polytope, also called a matroid basis polytope (or basis matroid polytope) to distinguish it from other polytopes derived from a matroid, is a polytope constructed via the bases of a matroid. Given a matroid , the matroid polytope is the convex hull of the indicator vectors of the bases of .
Definition
Let be a matroid on elements. Given a basis of , the indicator vector of is
where is the standard th unit vector in . The matroid polytope is the convex hull of the set
Examples

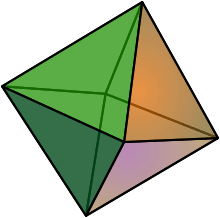
- Let be the rank 2 matroid on 4 elements with bases
- That is, all 2-element subsets of except . The corresponding indicator vectors of are
- The matroid polytope of is
- which is the square pyramid.
- Let be the rank 2 matroid on 4 elements with bases that are all 2-element subsets of . The corresponding matroid polytope is the octahedron. Observe that the polytope from the previous example is contained in .
- If is the uniform matroid of rank on elements, then the matroid polytope is the hypersimplex .[1]
Properties
- A matroid polytope is contained in the hypersimplex , where is the rank of the associated matroid and is the size of the ground set of the associated matroid.[2] More precisely, the vertices of are a subset of the vertices of .
- Every edge of a matroid polytope is a parallel translate of for some , the ground set of the associated matroid. In other words, the edges of correspond exactly to the pairs of bases that satisfy the basis exchange property: for some [2]
- Matroid polytopes are members of the family of generalized permutohedra.[3]
- Let be the rank function of a matroid . The matroid polytope can be written uniquely as a signed Minkowski sum of simplices:[3]
- where is the ground set of the matroid and is the signed beta invariant of :
Related polytopes
Independence matroid polytope
The matroid independence polytope or independence matroid polytope is the convex hull of the set
The (basis) matroid polytope is a face of the independence matroid polytope. Given the rank of a matroid , the independence matroid polytope is equal to the polymatroid determined by .
Flag matroid polytope
The flag matroid polytope is another polytope constructed from the bases of matroids. A flag is a strictly increasing sequence
of finite sets.[4] Let be the cardinality of the set . Two matroids and are said to be concordant if their rank functions satisfy
Given pairwise concordant matroids on the ground set with ranks , consider the collection of flags where is a basis of the matroid and . Such a collection of flags is a flag matroid . The matroids are called the constituents of . For each flag in a flag matroid , let be the sum of the indicator vectors of each basis in
Given a flag matroid , the flag matroid polytope is the convex hull of the set
A flag matroid polytope can be written as a Minkowski sum of the (basis) matroid polytopes of the constituent matroids:[4]
References
- ↑ Grötschel, Martin (2004), "Cardinality homogeneous set systems, cycles in matroids, and associated polytopes", The Sharpest Cut: The Impact of Manfred Padberg and His Work, MPS/SIAM Ser. Optim., SIAM, Philadelphia, PA, pp. 99–120, MR 2077557. See in particular the remarks following Prop. 8.20 on p. 114.
- 1 2 Gelfand, I.M.; Goresky, R.M.; MacPherson, R.D.; Serganova, V.V. (1987). "Combinatorial geometries, convex polyhedra, and Schubert cells". Advances in Mathematics. 63 (3): 301–316. doi:10.1016/0001-8708(87)90059-4.
- 1 2 Ardila, Federico; Benedetti, Carolina; Doker, Jeffrey (2010). "Matroid polytopes and their volumes". Discrete and Computational Geometry. 43 (4): 841–854. arXiv:0810.3947
 . doi:10.1007/s00454-009-9232-9.
. doi:10.1007/s00454-009-9232-9. - 1 2 Borovik, Alexandre V.; Gelfand, I.M.; White, Neil (2013). "Coxeter Matroids". Progress in Mathematics. 216. doi:10.1007/978-1-4612-2066-4.