Local Bubble
| Superbubble | |
|---|---|
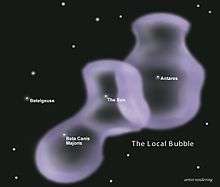 Artist's conception of the Local Bubble (containing the Sun and Beta Canis Majoris) and the Loop I Bubble (containing Antares) | |
| Observation data | |
| Distance | 0 ly (0 pc) |
| Physical characteristics | |
| Radius | 150 ly |
| Designations | Local Hot Bubble, LHB,[1] Local Bubble, Local Interstellar Bubble[2] |
The Local Bubble is a cavity in the interstellar medium (ISM) in the Orion Arm of the Milky Way. It contains, among others, the Local Interstellar Cloud, which contains the Solar System, and the G-cloud. It is at least 300 light years across and has a neutral-hydrogen density of about 0.05 atoms/cm3, or approximately one tenth of the average for the ISM in the Milky Way (0.5 atoms/cm3), and one sixth that of the Local Interstellar Cloud (0.3 atoms/cm3).[3] The hot diffuse gas in the Local Bubble emits X-rays.
The very sparse, hot gas of the Local Bubble is the result of supernovae that exploded within the past ten to twenty million years.[4][5] It was once thought that the most likely candidate for the remains of this supernova was Geminga ("Gemini gamma-ray source"), a pulsar in the constellation Gemini. Later, however, it has been suggested that multiple supernovae in subgroup B1 of the Pleiades moving group were more likely responsible,[6] becoming a remnant supershell.[7]
Description

The Solar System has been traveling through the region currently occupied by the Local Bubble for the last five to ten million years.[4] Its current location lies in the Local Interstellar Cloud (LIC), a minor region of denser material within the Bubble. The LIC formed where the Local Bubble and the Loop I Bubble met. The gas within the LIC has a density of approximately 0.1 atoms per cubic centimeter.
The Local Bubble is not spherical, but seems to be narrower in the galactic plane, becoming somewhat egg-shaped or elliptical, and may widen above and below the galactic plane, becoming shaped like an hourglass. It abuts other bubbles of less dense interstellar medium (ISM), including, in particular, the Loop I Bubble. The Loop I Bubble was created by supernovae and stellar winds in the Scorpius–Centaurus Association, some 500 light years from the Sun. The Loop I Bubble contains the star Antares (also known as Alpha Scorpii), as shown on the diagram above right. Several tunnels connect the cavities of the Local Bubble with the Loop I Bubble, called the "Lupus Tunnel".[8] Other bubbles which are adjacent to the Local Bubble are the Loop II Bubble and the Loop III Bubble.
Observation
Launched in February 2003 and active until April 2008, a small space observatory called Cosmic Hot Interstellar Plasma Spectrometer (CHIPS or CHIPSat) examined the hot gas within the Local Bubble.[9] The Local Bubble was also the region of interest for the Extreme Ultraviolet Explorer mission (1992–2001), which examined hot EUV sources within the bubble. Sources beyond the edge of the bubble were identified, but attenuated by the denser interstellar medium.
See also
- Gould Belt
- List of nearest stars and brown dwarfs
- Orion–Eridanus Superbubble
- Perseus Arm
- Superbubble
References
- ↑ Roland J. Egger, Bernd Aschenbach (February 1995). "Interaction of the Loop I supershell with the Local Hot Bubble". Astronomy and Astrophysics. 294 (2): L25-L28. arXiv:astro-ph/9412086
 . Bibcode:1995A&A...294L..25E.
. Bibcode:1995A&A...294L..25E. - ↑ "NAME LOCAL BUBBLE -- Interstellar matter". SIMBAD. Retrieved 15 March 2014.
- ↑ "Our Local Galactic Neighborhood, NASA". Interstellar.jpl.nasa.gov. 2000-02-08. Retrieved 2013-07-23.
- 1 2 Local Chimney and Superbubbles, Solstation.com
- ↑ NASA-funded X-ray Instrument Settles Interstellar Debate, www.nasa.gov
- ↑ T. W. Berghoefer; D. Breitschwerdt (2002). "The origin of the young stellar population in the solar neighborhood - a link to the formation of the Local Bubble?". Astronomy and Astrophysics. 390 (1): 299–306. arXiv:astro-ph/0205128v2
 . Bibcode:2002A&A...390..299B. doi:10.1051/0004-6361:20020627.
. Bibcode:2002A&A...390..299B. doi:10.1051/0004-6361:20020627. - ↑ J. R. Gabel, F. C. Bruhweiler (8 January 1998). "[51.09] Model of an Expanding Supershell Structure in the LISM". American Astronomical Society. Retrieved 2014-03-14.
- ↑ Lallement, R.; Welsh, B. Y.; Vergely, J. L.; Crifo, F.; Sfeir, D. (2003). "3D mapping of the dense interstellar gas around the Local Bubble". Astronomy and Astrophysics. 411 (3): 447–464. Bibcode:2003A&A...411..447L. doi:10.1051/0004-6361:20031214.
- ↑ "CHIPS - Berkeley University". Chips.ssl.berkeley.edu. 2003-01-12. Retrieved 2013-07-23.
Further reading
- Anderson, Mark (6 January 2007). "Don't stop till you get to the Fluff". New Scientist. 193 (2585): 26–30. doi:10.1016/S0262-4079(07)60043-8.
- Lallement, R.; Welsh, B. Y.; Vergely, J. L.; Crifo, F.; Sfeir, D. (December 1, 2003). "3D mapping of the dense interstellar gas around the Local Bubble". Astronomy & Astrophysics. 411 (3): 447–464. Bibcode:2003A&A...411..447L. doi:10.1051/0004-6361:20031214.
- "Near-Earth Supernovas". Science@NASA Headline News. NASA. January 6, 2003.
- "A Breeze from the Stars". Science@NASA Headline News. NASA. December 17, 2004.