Icosagon

Regular icosagon

A regular icosagon
Type Regular polygon
Edges and vertices 20
Schläfli symbol {20}, t{10}, tt{5}
Coxeter diagram
Symmetry group Dihedral (D20), order 2×20
Internal angle (degrees) 162°
Dual polygon Self
Properties Convex, cyclic, equilateral, isogonal, isotoxal

In geometry, an icosagon or 20-gon is a twenty-sided polygon. The sum of any icosagon's interior angles is 3240 degrees.

Regular icosagon

The regular icosagon has Schläfli symbol {20}, and can also be constructed as a truncated decagon, t{10}, or a twice-truncated pentagon, tt{5}.

One interior angle in a regular icosagon is 162°, meaning that one exterior angle would be 18°.

The area of a regular icosagon with edge length t is

In terms of the radius R of its circumcircle, the area is

since the area of the circle is the regular icosagon fills approximately 98.36% of its circumcircle.

Uses

The Big Wheel on the popular US game show The Price Is Right has an icosagonal cross-section.

The Globe, the outdoor theater used by William Shakespeare's acting company, was discovered to have been built on an icosagonal foundation when a partial excavation was done in 1989.[1]

As a golygonal path, the swastika is considered to be an irregular icosagon.[2]

A regular square, pentagon, and icosagon can completely fill a plane vertex.

Construction

As 20 = 22 × 5, regular icosagon is constructible using a compass and straightedge, or by an edge-bisection of a regular decagon, or a twice-bisected regular pentagon:


Construction of a regular icosagon
Construction of a regular decagon

The golden ratio in icosagon

Icosagon with given side length, animation (The construction is very similar to that of decagon with given side length)

Symmetry

Symmetries of a regular icosagon. Vertices are colored by their symmetry positions. Blue mirrors are drawn through vertices, and purple mirrors are drawn through edge. Gyration orders are given in the center.

The regular icosagon has Dih20 symmetry, order 40. There are 5 subgroup dihedral symmetries: (Dih10, Dih5), and (Dih4, Dih2, and Dih1), and 6 cyclic group symmetries: (Z20, Z10, Z5), and (Z4, Z2, Z1).

These 10 symmetries can be seen in 16 distinct symmetries on the icosagon, a larger number because the lines of reflections can either pass through vertices or edges. John Conway labels these by a letter and group order.[3] Full symmetry of the regular form is r40 and no symmetry is labeled a1. The dihedral symmetries are divided depending on whether they pass through vertices (d for diagonal) or edges (p for perpendiculars), and i when reflection lines path through both edges and vertices. Cyclic symmetries in the middle column are labeled as g for their central gyration orders.

Each subgroup symmetry allows one or more degrees of freedom for irregular forms. Only the g20 subgroup has no degrees of freedom but can seen as directed edges.

The highest symmetry irregular icosagons are d20, a isogonal icosagon constructed by ten mirrors which can alternate long and short edges, and p20, an isotoxal icosagon, constructed with equal edge lengths, but vertices alternating two different internal angles. These two forms are duals of each other and have half the symmetry order of the regular icosagon.

Related polygons

An icosagram is a 20-sided star polygon, represented by symbol {20/n}. There are three regular forms given by Schläfli symbols: {20/3}, {20/7}, and {20/9}. There are also five regular star figures (compounds) using the same vertex arrangement: 2{10}, 4{5}, 5{4}, 2{10/3}, 4{5/2}, and 10{2}.

n 1 2 3 4 5
Form Convex polygon Compound Star polygon Compound
Image
{20/1} = {20}
{20/2} = 2{10}
{20/3}
{20/4} = 4{5}
{20/5} = 5{4}
Interior angle 162° 144° 126° 108° 90°
n 6 7 8 9 10
Form Compound Star polygon Compound Star polygon Compound
Image
{20/6} = 2{10/3}
{20/7}
{20/8} = 4{5/2}
{20/9}
{20/10} = 10{2}
Interior angle 72° 54° 36° 18° 0°

Deeper truncations of the regular decagon and decagram can produce isogonal (vertex-transitive) intermediate icosagram forms with equally spaced vertices and two edge lengths.[4]

A regular icosagram, {20/9}, can be seen as a quasitruncated decagon, t{10/9}={20/9}. Similarly a decagram, {10/3} has a quasitruncation t{10/7}={20/7}, and finally a simple truncation of a decagram gives t{10/3}={20/3}.

Icosagrams as truncations of a regular decagons and decagrams, {10}, {10/3}
Quasiregular Quasiregular

t{10}={20}
t{10/9}={20/9}

t{10/3}={20/3}
t{10/7}={20/7}

Petrie polygons

The regular icosagon is the Petrie polygon for a number of higher-dimensional polytopes, shown in orthogonal projections in Coxeter planes:

A19 B10 D11 E8 H4 2H2

19-simplex
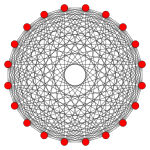10-orthoplex
10-cube
11-demicube
(421)
600-cell
10-10 duopyramid
10-10 duoprism

It is also the Petrie polygon for the icosahedral 120-cell, small stellated 120-cell, great icosahedral 120-cell, and great grand 120-cell.

References

  1. ↑ Muriel Pritchett, University of Georgia "To Span the Globe", see also Editor's Note, retrieved on 10th January 2016
  2. ↑ Weisstein, Eric W. "Icosagon". MathWorld.
  3. ↑ John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss, (2008) The Symmetries of Things, ISBN 978-1-56881-220-5 (Chapter 20, Generalized Schaefli symbols, Types of symmetry of a polygon pp. 275-278)
  4. ↑ The Lighter Side of Mathematics: Proceedings of the Eugène Strens Memorial Conference on Recreational Mathematics and its History, (1994), Metamorphoses of polygons, Branko Grünbaum
This article is issued from Wikipedia - version of the 10/31/2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.