Hsu–Robbins–Erdős theorem

In the mathematical theory of probability, the Hsu–Robbins–Erdős theorem states that if $X_1, \ldots ,X_n$ is a sequence of i.i.d. random variables with zero mean and finite variance and

S_n = X_1 + \cdots + X_n, \,

then

\sum\limits_{n \geqslant 1} P( | S_n | > \varepsilon n) < \infty

for every $\varepsilon > 0$ .

The result was proved by Pao-Lu Hsu and Herbert Robbins in 1947.

This is an interesting strengthening of the classical strong law of large numbers in the direction of the Borel–Cantelli lemma. The idea of such a result is probably due to Robbins, but the method of proof is vintage Hsu.^[1] Hsu and Robbins further conjectured in ^[2] that the condition of finiteness of the variance of 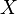$X$ is also a necessary condition for $\sum\limits_{n \geqslant 1} P(| S_n | > \varepsilon n) < \infty$ to hold. Two years later, the famed mathematician Paul Erdős proved the conjecture.^[3]

Since then, many authors extended this result in several directions.^[4]

References

↑ Chung, K. L. (1979). Hsu's work in probability. The Annals of Statistics, 479–483.
↑ Hsu, P. L., & Robbins, H. (1947). Complete convergence and the law of large numbers. Proceedings of the National Academy of Sciences of the United States of America, 33(2), 25.
↑ Erdos, P. (1949). On a theorem of Hsu and Robbins. The Annals of Mathematical Statistics, 286–291.
↑ Hsu-Robbins theorem for the correlated sequences

This article is issued from Wikipedia - version of the 1/24/2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.