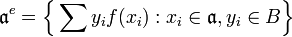Extension and contraction of ideals

In commutative algebra, the extension and contraction of ideals are operations performed on sets of ideals.

Extension of an ideal

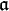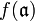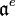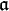Let A and B be two commutative rings with unity, and let f : A → B be a (unital) ring homomorphism. If $\mathfrak{a}$ is an ideal in A, then $f(\mathfrak{a})$ need not be an ideal in B (e.g. take f to be the inclusion of the ring of integers Z into the field of rationals Q). The extension $\mathfrak{a}^e$ of $\mathfrak{a}$ in B is defined to be the ideal in B generated by 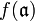$f(\mathfrak{a})$ . Explicitly,

\mathfrak{a}^e = \Big\{ \sum y_if(x_i) : x_i \in \mathfrak{a}, y_i \in B \Big\}

Contraction of an ideal

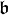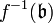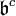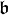If $\mathfrak{b}$ is an ideal of B, then $f^{-1}(\mathfrak{b})$ is always an ideal of A, called the contraction $\mathfrak{b}^c$ of $\mathfrak{b}$ to A.

Properties

Assuming f : A → B is a unital ring homomorphism, 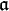$\mathfrak{a}$ is an ideal in A, 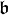$\mathfrak{b}$ is an ideal in B, then:

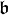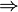
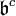$\mathfrak{b}$ is prime in B $\Rightarrow$ $\mathfrak{b}^c$ is prime in A.
$\mathfrak{a}^{ec} \supseteq \mathfrak{a}$
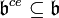
$\mathfrak{b}^{ce} \subseteq \mathfrak{b}$

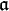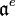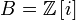It is false, in general, that $\mathfrak{a}$ being prime (or maximal) in A implies that $\mathfrak{a}^e$ is prime (or maximal) in B. Many classic examples of this stem from algebraic number theory. For example, embedding $\mathbb{Z} \to \mathbb{Z}\left\lbrack i \right\rbrack$ . In $B = \mathbb{Z}\left\lbrack i \right\rbrack$ , the element 2 factors as 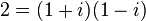$2 = (1 + i)(1 - i)$ where (one can show) neither of 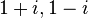$1 + i, 1 - i$ are units in B. So $(2)^e$ is not prime in B (and therefore not maximal, as well). 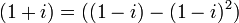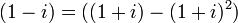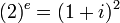Indeed, $(1 \pm i)^2 = \pm 2i$ shows that $(1 + i) = ((1 - i) - (1 - i)^2)$ , $(1 - i) = ((1 + i) - (1 + i)^2)$ , and therefore $(2)^e = (1 + i)^2$ .

On the other hand, if f is surjective and $\mathfrak{a} \supseteq \mathop{\mathrm{ker}} f$ then:

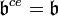$\mathfrak{a}^{ec}=\mathfrak{a}$ and $\mathfrak{b}^{ce}=\mathfrak{b}$ .
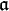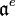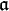$\mathfrak{a}$ is a prime ideal in A $\Leftrightarrow$ $\mathfrak{a}^e$ is a prime ideal in B.
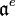$\mathfrak{a}$ is a maximal ideal in A $\Leftrightarrow$ $\mathfrak{a}^e$ is a maximal ideal in B.

Extension of prime ideals in number theory

Let K be a field extension of L, and let B and A be the rings of integers of K and L, respectively. Then B is an integral extension of A, and we let f be the inclusion map from A to B. The behaviour of a prime ideal 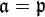$\mathfrak{a} = \mathfrak{p}$ of A under extension is one of the central problems of algebraic number theory.

References

Atiyah, M. F. and Macdonald, I. G., Introduction to Commutative Algebra, Perseus Books, 1969, ISBN 0-201-00361-9

This article is issued from Wikipedia - version of the 3/19/2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.