Estimation lemma

In mathematics the estimation lemma, also known as the M-L inequality, gives an upper bound for a contour integral. If $f$ is a complex-valued, continuous function on the contour $Γ$ and if its absolute value $| f (z)|$ is bounded by a constant $M$ for all $z$ on $Γ$ , then

\left|\int _{\Gamma }f(z)\,dz\right|\leq M\,l(\Gamma ),

where $l (Γ)$ is the arc length of $Γ$ . In particular, we may take the maximum

M:=\max _{{z\in \Gamma }}|f(z)|

as upper bound. Intuitively, the lemma is very simple to understand. If a contour is thought of as many smaller contour segments connected together, then there will be a maximum $| f (z)|$ for each segment. Out of all the maximum $| f (z)|$ s for the segments, there will be an overall largest one. Hence, if the overall largest $| f (z)|$ is summed over the entire path then the integral of $f (z)$ over the path must be less than or equal to it.

Formally, the inequality can be shown to hold using the definition of contour integral, the absolute value inequality for integrals and the formula for the length of a curve as follows:

{\biggl |}\int _{\Gamma }f(z)\,dz{\biggr |}={\biggl |}\int _{\alpha }^{\beta }f(\gamma (t))\gamma '(t)\,dt{\biggr |}\leq \int _{\alpha }^{\beta }\left|f(\gamma (t))\right|\left|\gamma '(t)\right|\,dt\leq M\int _{\alpha }^{\beta }\left|\gamma '(t)\right|\,dt=M\,l(\Gamma )

The estimation lemma is most commonly used as part of the methods of contour integration with the intent to show that the integral over part of a contour goes to zero as $| z |$ goes to infinity. An example of such a case is shown below.

Example

The contour

Γ

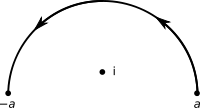
Problem. Find an upper bound for

{\biggl |}\int _{\Gamma }{\frac {1}{(z^{2}+1)^{2}}}\,dz{\biggr |},

where $Γ$ is the upper half-circle $| z | = a$ with radius $a > 1$ traversed once in the counterclockwise direction.

Solution. First observe that the length of the path of integration is half the circumference of a circle with radius $a$ , hence

l(\Gamma )={\frac {1}{2}}(2\pi a)=\pi a.

Next we seek an upper bound $M$ for the integrand when $| z | = a$ . By the triangle inequality we see that

|z|^{2}=|z^{2}|=|z^{2}+1-1|\leq |z^{2}+1|+1,

therefore

|z^{2}+1|\geq |z|^{2}-1=a^{2}-1>0

because $| z | = a > 1$ on $Γ$ . Hence

\left|{\frac {1}{(z^{2}+1)^{2}}}\right|\leq {\frac {1}{(a^{2}-1)^{2}}}.

Therefore we apply the estimation lemma with $M = 1 / (a 2 - 1) 2$ . The resulting bound is

{\biggl |}\int _{\Gamma }{\frac {1}{(z^{2}+1)^{2}}}\,dz{\biggr |}\leq {\frac {\pi a}{(a^{2}-1)^{2}}}.

References

Saff, E.B; Snider, A.D. (1993), Fundamentals of Complex Analysis for Mathematics, Science, and Engineering (2nd ed.), Prentice Hall, ISBN 978-0133274615 .
Howie, J.M. (2003), Complex Analysis, Springer .

This article is issued from Wikipedia - version of the 12/16/2014. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.

Estimation lemma

Example

See also

References