Curie temperature


In physics and materials science, the Curie temperature (TC), or Curie point, is the temperature at which certain materials lose their permanent magnetic properties, to be replaced by induced magnetism. The Curie temperature is named after Pierre Curie, who showed that magnetism was lost at a critical temperature.[1]
The force of magnetism is determined by the magnetic moment, a dipole moment within an atom which originates from the angular momentum and spin of electrons. Materials have different structures of intrinsic magnetic moments that depend on temperature; the Curie temperature is the critical point at which a material's intrinsic magnetic moments change direction.
Permanent magnetism is caused by the alignment of magnetic moments and induced magnetism is created when disordered magnetic moments are forced to align in an applied magnetic field. For example, the ordered magnetic moments (ferromagnetic, Figure 1) change and become disordered (paramagnetic, Figure 2) at the Curie temperature. Higher temperatures make magnets weaker, as spontaneous magnetism only occurs below the Curie temperature. Magnetic susceptibility above the Curie Temperature can be calculated from the Curie–Weiss law, which is derived from Curie's law.
In analogy to ferromagnetic and paramagnetic materials, the Curie temperature can also be used to describe the phase transition between ferroelectricity and paraelectricity. In this context, the order parameter is the electric polarisation that goes from a finite value to zero when the temperature is increased above the Curie temperature.
| Material | Curie temperature (K) |
|---|---|
| Iron (Fe) | 1043 |
| Cobalt (Co) | 1400 |
| Nickel (Ni) | 627 |
| Gadolinium (Gd) | 292 |
| Dysprosium (Dy) | 88 |
| Manganese bismuthide (MnBi) | 630 |
| Manganese antimonide (MnSb) | 587 |
| Chromium(IV) oxide (CrO2) | 386 |
| Manganese arsenide (MnAs) | 318 |
| Europium oxide (EuO) | 69 |
| Iron(III) oxide (Fe2O3) | 948 |
| Iron(II,III) oxide (FeOFe2O3) | 858 |
| NiO–Fe2O3 | 858 |
| CuO–Fe2O3 | 728 |
| MgO–Fe2O3 | 713 |
| MnO–Fe2O3 | 573 |
| Yttrium iron garnet (Y3Fe5O12) | 560 |
| Neodymium magnets | 583–673 |
| Alnico | 973–1133 |
| Samarium–cobalt magnets | 993–1073 |
| Strontium ferrite | 723 |
Magnetic moments
Magnetic moments are permanent dipole moments within the atom which are made up from electrons' angular momentum and spin.[5]
Electrons inside atoms contribute magnetic moments from their own angular momentum and from their orbital momentum around the nucleus. Magnetic moments from the nucleus are insignificant in contrast to magnetic moments from electrons.[6] Thermal contribution will result in higher energy electrons causing disruption to their order and alignment between dipoles to be destroyed.
Ferromagnetic, paramagnetic, ferrimagnetic and antiferromagnetic materials have different structures of intrinsic magnetic moments. It is at a material's specific Curie temperature where they change properties. The transition from antiferromagnetic to paramagnetic (or vice versa) occurs at the Néel temperature which is analogous to Curie temperature.
| Below TC | Above TC |
|---|---|
| Ferromagnetic | ↔ Paramagnetic |
| Ferrimagnetic | ↔ Paramagnetic |
| Antiferromagnetic | ↔ Paramagnetic |
- Orientations of magnetic moments in materials
-

Ferromagnetism: The magnetic moments in a ferromagnetic material. The moments are ordered and of the same magnitude in the absence of an applied magnetic field.
-

Paramagnetism: The magnetic moments in a paramagnetic material. The moments are disordered in the absence of an applied magnetic field and ordered in the presence of an applied magnetic field.
-

Ferrimagnetism: The magnetic moments in a ferrimagnetic material. The moments are aligned oppositely and have different magnitudes due to being made up of two different ions. This is in the absence of an applied magnetic field.
-

Antiferromagnetism: The magnetic moments in an antiferromagnetic material. The moments are aligned oppositely and have the same magnitudes. This is in the absence of an applied magnetic field.
Materials with magnetic moments that change properties at the Curie temperature
Ferromagnetic, paramagnetic, ferrimagnetic and antiferromagnetic structures are made up of intrinsic magnetic moments. If all electrons within the structure are paired, these moments cancel out due to having opposite spins and angular momentum. Thus even with an applied magnetic field will have different properties and no Curie temperature.[7][8]
Paramagnetic
A material is paramagnetic only above its Curie temperature. Paramagnetic materials are non-magnetic when a magnetic field is absent and magnetic when a magnetic field is applied. When the magnetic field is absent the material has disordered magnetic moments; that is, the atoms are asymmetrical and not aligned. When the magnetic field is present the magnetic moments are temporarily realigned parallel to the applied field;[9][10] the atoms are symmetrical and aligned.[11] The magnetic moment in the same direction is what causes an induced magnetic field.[11][12]
For paramagnetism this response to an applied magnetic field is positive and known as magnetic susceptibility.[7] The magnetic susceptibility only applies above the Curie temperature for disordered states.[13]
Sources of paramagnetism (materials which have Curie temperatures) include:[14]
- All atoms which have unpaired electrons;
- Atoms where inner shells are incomplete in electrons;
- Free radicals;
- Metals.
Above the Curie temperature the atoms are excited, the spin orientation becomes randomised,[8] but can be realigned in an applied field, i.e. the material becomes paramagnetic. Below the Curie temperature the intrinsic structure has undergone a phase transition,[15] the atoms are ordered and the material is ferromagnetic.[11] The paramagnetic materials' induced magnetic fields are very weak in comparison to ferromagnetic materials' magnetic fields.[15]
Ferromagnetic
Materials are only ferromagnetic below their corresponding Curie temperatures. Ferromagnetic materials are magnetic in the absence of an applied magnetic field.
When a magnetic field is absent the material has spontaneous magnetization which is a result of the ordered magnetic moments; that is, for ferromagnetism, the atoms are symmetrical and aligned in the same direction creating a permanent magnetic field.
The magnetic interactions are held together by exchange interactions; otherwise thermal disorder would overcome the weak interactions of magnetic moments. The exchange interaction has a zero probability of parallel electrons occupying the same point in time, implying a preferred parallel alignment in the material.[16] The Boltzmann factor contributes heavily as it prefers interacting particles to be aligned in the same direction.[17] This causes ferromagnets to have strong magnetic fields and high Curie temperatures of around 1000 K.[18]
Below the Curie temperature, the atoms are aligned and parallel, causing spontaneous magnetism; the material is ferromagnetic. Above the Curie temperature the material is paramagnetic, as the atoms lose their ordered magnetic moments when the material undergoes a phase transition.[15]
Ferrimagnetic
Materials are only ferrimagnetic below their corresponding Curie temperature. Ferrimagnetic materials are magnetic in the absence of an applied magnetic field and are made up of two different ions.[19]
When a magnetic field is absent the material has a spontaneous magnetism which is the result of ordered magnetic moments; that is, for ferrimagnetism one ion's magnetic moments are aligned facing in one direction with certain magnitude and the other ion's magnetic moments are aligned facing in the opposite direction with a different magnitude. As the magnetic moments are of different magnitudes in opposite directions there is still a spontaneous magnetism and a magnetic field is present.[19]
Similar to ferromagnetic materials the magnetic interactions are held together by exchange interactions. The orientations of moments however are anti-parallel which results in a net momentum by subtracting their momentum from one another.[19]
Below the Curie temperature the atoms of each ion are aligned anti-parallel with different momentums causing a spontaneous magnetism; the material is ferrimagnetic. Above the Curie temperature the material is paramagnetic as the atoms lose their ordered magnetic moments as the material undergoes a phase transition.[19]
Antiferromagnetic and the Néel temperature
Materials are only antiferromagetic below their corresponding Néel temperature. This is similar to the Curie temperature as above the Néel Temperature the material undergoes a phase transition and becomes paramagnetic.
The material has equal magnetic moments aligned in opposite directions resulting in a zero magnetic moment and a net magnetism of zero at all temperatures below the Néel temperature. Antiferromagnetic materials are weakly magnetic in the absence or presence of an applied magnetic field.
Similar to ferromagnetic materials the magnetic interactions are held together by exchange interactions preventing thermal disorder from overcoming the weak interactions of magnetic moments.[16][20] When disorder occurs it is at the Néel temperature.[20]
Curie–Weiss law
The Curie–Weiss law is an adapted version of Curie's law.
The Curie–Weiss law is a simple model derived from a mean-field approximation, this means it works well for the materials temperature, T, much greater than their corresponding Curie temperature, TC, i.e. T ≫ TC; however fails to describe the magnetic susceptibility, χ, in the immediate vicinity of the Curie point because of local fluctuations between atoms.[21]
Neither Curie's law nor the Curie–Weiss law holds for T < TC.
Curie's law for a paramagnetic material:[22]
| Definition | |
|---|---|
| χ | the magnetic susceptibility; the influence of an applied magnetic field on a material |
| M | the magnetic moments per unit volume |
| H | the macroscopic magnetic field |
| B | the magnetic field |
| C | the material-specific Curie constant |
| µ0 | the permeability of free space. Note: in CGS units is taken to equal one.[24] |
| g | the Landé g-factor |
| J(J + 1) | the eigenvalue for eigenstate J2 for the stationary states within the incomplete atoms shells (electrons unpaired) |
| µB | the Bohr Magneton |
| kB | Boltzmann's constant |
| total magnetism | is N number of magnetic moments per unit volume |
The Curie–Weiss law is then derived from Curie's law to be:
where:
λ is the Weiss molecular field constant.[23][25]
For full derivation see Curie–Weiss law.
Physics
Approaching Curie temperature from above
As the Curie–Weiss law is an approximation, a more accurate model is needed when the temperature, T, approaches the material's Curie temperature, TC.
Magnetic susceptibility occurs above the Curie temperature.
An accurate model of critical behaviour for magnetic susceptibility with critical exponent γ:
The critical exponent differs between materials and for the mean-field model is taken as γ = 1.[26]
As temperature is inversely proportional to magnetic susceptibility, when T approaches TC the denominator tends to zero and the magnetic susceptibility approaches infinity allowing magnetism to occur. This is a spontaneous magnetism which is a property of ferromagnetic and ferrimagnetic materials.[27][28]
Approaching Curie temperature from below
Magnetism depends on temperature and spontaneous magnetism occurs below the Curie temperature. An accurate model of critical behaviour for spontaneous magnetism with critical exponent β:
The critical exponent differs between materials and for the mean-field model as taken as β = 1/2 where T ≪ TC.[26]
The spontaneous magnetism approaches zero as the temperature increases towards the materials Curie temperature.
Approaching absolute zero (0 kelvins)
The spontaneous magnetism, occurring in ferromagnetic, ferrimagnetic and antiferromagnetic materials, approaches zero as the temperature increases towards the material's Curie temperature. Spontaneous magnetism is at its maximum as the temperature approaches 0 K.[29] That is, the magnetic moments are completely aligned and at their strongest magnitude of magnetism due to no thermal disturbance.
In paramagnetic materials temperature is sufficient to overcome the ordered alignments. As the temperature approaches 0 K, the entropy decreases to zero, that is, the disorder decreases and becomes ordered. This occurs without the presence of an applied magnetic field and obeys the third law of thermodynamics.[16]
Both Curie's law and the Curie–Weiss law fail as the temperature approaches 0 K. This is because they depend on the magnetic susceptibility which only applies when the state is disordered.[30]
Gadolinium sulphate continues to satisfy Curie's law at 1 K. Between 0 and 1 K the law fails to hold and a sudden change in the intrinsic structure occurs at the Curie temperature.[31]
Ising model of phase transitions
The Ising model is mathematically based and can analyse the critical points of phase transitions in ferromagnetic order due to spins of electrons having magnitudes of ±1/2. The spins interact with their neighbouring dipole electrons in the structure and here the Ising model can predict their behaviour with each other.[32][33]
This model is important for solving and understanding the concepts of phase transitions and hence solving the Curie temperature. As a result, many different dependencies that effect the Curie temperature can be analysed.
For example, the surface and bulk properties depend on the alignment and magnitude of spins and the Ising model can determine the effects of magnetism in this system.
Weiss domains and surface and bulk Curie temperatures

Materials structures consist of intrinsic magnetic moments which are separated into domains called Weiss domains.[34] This can result in ferromagnetic materials having no spontaneous magnetism as domains could potentially balance each other out.[34] The position of particles can therefore have different orientations around the surface than the main part (bulk) of the material. This property directly affects the Curie temperature as there can be a bulk Curie temperature TB and a different surface Curie temperature TS for a material.[35]
This allows for the surface Curie temperature to be ferromagnetic above the bulk Curie temperature when the main state is disordered, i.e. Ordered and disordered states occur simultaneously.[32]
The surface and bulk properties can be predicted by the Ising model and electron capture spectroscopy can be used to detect the electron spins and hence the magnetic moments on the surface of the material. An average total magnetism is taken from the bulk and surface temperatures to calculate the Curie temperature from the material, noting the bulk contributes more.[32][36]
The angular momentum of an electron is either +ħ/2 or −ħ/2 due to it having a spin of 1/2, which gives a specific size of magnetic moment to the electron; the Bohr magneton.[37] Electrons orbiting around the nucleus in a current loop create a magnetic field which depends on the Bohr Magneton and magnetic quantum number.[37] Therefore, the magnetic moments are related between angular and orbital momentum and affect each other. Angular momentum contributes twice as much to magnetic moments than orbital.[38]
For terbium which is a rare earth metal and has a high orbital angular momentum the magnetic moment is strong enough to affect the order above its bulk temperatures. It is said to have a high anisotropy on the surface, that is it is highly directed in one orientation. It remains ferromagnetic on its surface above its Curie temperature while its bulk becomes ferrimagnetic and then at higher temperatures its surface remains ferrimagnetic above its bulk Néel Temperature before becoming completely disordered and paramagnetic with increasing temperature. The anisotropy in the bulk is different from its surface anisotropy just above these phase changes as the magnetic moments will be ordered differently or ordered in paramagnetic materials.[35]
Changing a material's Curie temperature
Composite materials
Composite materials, that is, materials composed from other materials with different properties, can change the Curie temperature. For example, a composite which has silver in it can create spaces for oxygen molecules in bonding which decreases the Curie temperature[39] as the crystal lattice will not be as compact.
The alignment of magnetic moments in the composite material affects the Curie temperature. If the materials moments are parallel with each other the Curie temperature will increase and if perpendicular the Curie temperature will decrease[39] as either more or less thermal energy will be needed to destroy the alignments.
Preparing composite materials through different temperatures can result in different final compositions which will have different Curie temperatures.[40] Doping a material can also affect its Curie temperature.[40]
The density of nanocomposite materials changes the Curie temperature. Nanocomposites are compact structures on a nano-scale. The structure is built up of high and low bulk Curie temperatures, however will only have one mean-field Curie temperature. A higher density of lower bulk temperatures results in a lower mean-field Curie temperature and a higher density of higher bulk temperature significantly increases the mean-field Curie temperature. In more than one dimension the Curie temperature begins to increase as the magnetic moments will need more thermal energy to overcome the ordered structure.[36]
Particle size
The size of particles in a material's crystal lattice changes the Curie temperature. Due to the small size of particles (nanoparticles) the fluctuations of electron spins become more prominent, this results in the Curie temperature drastically decreasing when the size of particles decrease as the fluctuations cause disorder. The size of a particle also affects the anisotropy causing alignment to become less stable and thus lead to disorder in magnetic moments.[32][41]
The extreme of this is superparamagnetism which only occurs in small ferromagnetic particles and is where fluctuations are very influential causing magnetic moments to change direction randomly and thus create disorder.
The Curie temperature of nanoparticles are also affected by the crystal lattice structure, body-centred cubic (bcc), face-centred cubic (fcc) and a hexagonal structure (hcp) all have different Curie temperatures due to magnetic moments reacting to their neighbouring electron spins. fcc and hcp have tighter structures and as a results have higher Curie temperatures than bcc as the magnetic moments have stronger effects when closer together.[32] This is known as the coordination number which is the number of nearest neighbouring particles in a structure. This indicates a lower coordination number at the surface of a material than the bulk which leads to the surface becoming less significant when the temperature is approaching the Curie temperature. In smaller systems the coordination number for the surface is more significant and the magnetic moments have a stronger affect on the system.[32]
Although fluctuations in particles can be minuscule, they are heavily dependent on the structure of crystal lattices as they react with their nearest neighbouring particles. Fluctuations are also affected by the exchange interaction[41] as parallel facing magnetic moments are favoured and therefore have less disturbance and disorder, therefore a tighter structure influences a stronger magnetism and therefore a higher Curie temperature.
Pressure
Pressure changes a material's Curie temperature. Increasing pressure on the crystal lattice decreases the volume of the system. Pressure directly affects the kinetic energy in particles as movement increases causing the vibrations to disrupt the order of magnetic moments. This is similar to temperature as it also increases the kinetic energy of particles and destroys the order of magnetic moments and magnetism.[42]
Pressure also affects the density of states (DOS).[42] Here the DOS decreases causing the number of electrons available to the system to decrease. This leads to the number of magnetic moments decreasing as they depend on electron spins. It would be expected because of this that the Curie temperature would decrease however it increases. This is the result of the exchange interaction. The exchange interaction favours the aligned parallel magnetic moments due to electrons being unable to occupy the same space in time[16] and as this is increased due to the volume decreasing the Curie temperature increases with pressure. The Curie temperature is made up of a combination of dependencies on kinetic energy and the DOS.[42]
It is interesting to note that the concentration of particles also affects the Curie temperature when pressure is being applied and can result in a decrease in Curie temperature when the concentration is above a certain percent.[42]
Orbital ordering
Orbital ordering changes the Curie temperature of a material. Orbital ordering can be controlled through applied strains.[43] This is a function that determines the wave of a single electron or paired electrons inside the material. Having control over the probability of where the electron will be allows the Curie temperature to be altered. For example, the delocalised electrons can be moved onto the same plane by applied strains within the crystal lattice.[43]
The Curie temperature is seen to increase greatly due to electrons being packed together in the same plane, they are forced to align due to the exchange interaction and thus increases the strength of the magnetic moments which prevents thermal disorder at lower temperatures.
Curie temperature in ferroelectric and piezoelectric materials
In analogy to ferromagnetic and paramagnetic materials, the Curie temperature can also be used to describe the temperature where a material's spontaneous electric polarisation changes to induced electric polarisation, or vice versa.[44]
Electric polarisation is a result of aligned electric dipoles. Aligned electric dipoles are composites of positive and negative charges where all the dipoles are facing in one direction. The charges are separated from their stable placement in the particles and can occur spontaneously, from pressure or an applied electric field.[45]
Ferroelectric, dielectric (paraelectric) and piezoelectric materials have electric polarisation. In ferroelectric materials there is a spontaneous electric polarisation in the absence of an applied electric field.[44] In dielectric materials there is electric polarisation aligned only when an electric field is applied.[45] Piezoelectric materials have electric polarisation due to applied mechanical stress distorting the structure from pressure.[46]
T0 is the temperature where ferroelectric materials lose their spontaneous polarisation as a first or second order phase change occurs, that is the internal structure changes or the internal symmetry changes.[44] In certain cases T0 is equal to the Curie temperature however the Curie temperature can be 10 kelvins lower than T0.[47]

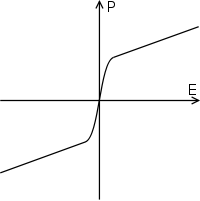
| Below T0 | Above T0[48] |
|---|---|
| Ferroelectric | ↔ Dielectric (paraelectric) |
All ferroelectric materials are pyroelectric[49] and piezoelectric,[50] but not the converse.
Piezoelectric
An external force applies pressure on particles inside the material which affects the structure of the crystal lattice. Particles in a unit cell become unsymmetrical which allows a net polarisation from each particle. Symmetry would cancel the opposing charges out and there would be no net polarisation.[51] Below the transition temperature T0 displacement of electric charges causes polarisation. Above the transition temperature T0 the structure is cubic and symmetric, causing the material to become dielectric. Electric charges are also agitated and disordered causing the material to have no electric polarisation in the absence of an applied electric field.
Ferroelectric and dielectric
Materials are only ferroelectric below their corresponding transition temperature T0.[44] Ferroelectric materials are all piezoelectric and therefore have a spontaneous electric polarisation as the structures are unsymmetrical.
Materials are only dielectric above their corresponding transition temperature T0.[52] Dielectric materials have no electric polarisation in the absence of an applied electric field. The electric dipoles are unaligned and have no net polarisation. In analogy to magnetic susceptibility, electric susceptibility only occurs above T0.
Ferroelectric materials when polarised are influenced under hysteresis (Figure 4); that is they are dependent on their past state as well as their current state. As an electric field is applied the dipoles are forced to align and polarisation is created, when the electric field is removed polarisation remains. The hysteresis loop depends on temperature and as a result as the temperature is increased and reaches T0 the two curves become one curve as shown in the dielectric polarisation (Figure 5).[53]
Relative permittivity
A modified version of the Curie–Weiss law applies to the dielectric constant, also known as the relative permittivity:[47][54]
Applications
A heat-induced ferromagnetic-paramagnetic transition is used in magneto-optical storage media, for erasing and writing of new data. Famous examples include the Sony Minidisc format, as well as the now-obsolete CD-MO format. Other uses include temperature control in soldering irons,[55] and stabilizing the magnetic field of tachometer generators against temperature variation.[56]
See also
Notes
- ↑ "Pierre Curie – Biography". Nobelprize.org. The Nobel Foundation 1903. Retrieved 14 March 2013.
- ↑ Buschow 2001, p5021, table 1
- ↑ Jullien 1989, p. 155
- ↑ Kittel 1986
- ↑ Hall 1994, p. 200
- ↑ Jullien 1989, pp. 136–138
- 1 2 Lüth, Harald Ibach, Hans (2009). Solid-state physics: an introduction to principles of materials science (4th extensively updated and enlarged ed.). Berlin: Springer. ISBN 978-3-540-93803-3.
- 1 2 Levy 1968, pp. 236–239
- ↑ Dekker 1958, pp. 217–220
- ↑ Levy 1968
- 1 2 3 Fan 1987, pp. 164–165
- ↑ Dekker 1958, pp. 454–455
- ↑ Mendelssohn 1977, p. 162
- ↑ Levy 1968, pp. 198–202
- 1 2 3 Cusack 1958, p. 269
- 1 2 3 4 Hall 1994, pp. 220–221
- ↑ Palmer 2007
- ↑ Hall 1994, p. 220
- 1 2 3 4 Jullien 1989, pp. 158–159
- 1 2 Jullien 1989, pp. 156–157
- ↑ Jullien 1989, pp. 153
- ↑ Hall 1994, pp. 205–206
- 1 2 Levy 1968, pp. 201–202
- ↑ Kittel 1996, pp. 444
- ↑ Myers 1997, pp. 334–345
- 1 2 Hall 1994, pp. 227–228
- ↑ Kittel 1986, pp. 424–426
- ↑ Spaldin 2010, pp. 52–54
- ↑ Hall 1994, pp. 225
- ↑ Mendelssohn 1977, pp. 180–181
- ↑ Mendelssohn 1977, p. 167
- 1 2 3 4 5 6 Bertoldi 2012
- ↑ Brout 1965, pp. 6–7
- 1 2 Jullien 1989, p. 161
- 1 2 Rau 1988
- 1 2 Skomski 2000
- 1 2 Jullien 1989, pp. 138
- ↑ Hall 1994
- 1 2 Hwang 1998
- 1 2 Jones 2003
- 1 2 López Domínguez 2012
- 1 2 3 4 Bose 2011
- 1 2 Sadoc 2010
- 1 2 3 4 Myers 1997, pp. 404–405
- 1 2 Jullien 1989, pp. 56–59
- ↑ Hall 1994, p. 275
- 1 2 Webster 1999
- ↑ Kovetz 1990, p. 116
- ↑ Whatmore 1991, pp. 283
- ↑ Myers 1991, pp. 449
- ↑ Pascoe 1973, pp. 186–187
- ↑ Hummel 2001, pp. 189
- ↑ Pascoe 1973, pp. 190–191
- ↑ Webster, John G. (1999). The measurement, instrumentation, and sensors handbook (Online ed.). Boca Raton, FL: CRC Press published in cooperation with IEEE Press. pp. 6.55–6.56. ISBN 9780849383472.
- ↑ "Thermaltronics Soldering: Products > TMT-9000S Soldering and Rework Station". thermaltronics.com. Retrieved 13 January 2016.
- ↑ Pallàs-Areny & Webster 2001, pp. 262–263
References
- Buschow, K. H. J. (2001). Encyclopedia of Materials: Science and Technology. Elsevier. ISBN 0-08-043152-6.
- Kittel, Charles (1986). Introduction to Solid State Physics (6th ed.). John Wiley & Sons. ISBN 0-471-87474-4.
- Pallàs-Areny, Ramon; Webster, John G. (2001). Sensors and Signal Conditioning (2nd ed.). John Wiley & Sons. pp. 262–263. ISBN 978-0-471-33232-9.
- Spaldin, Nicola A. (2010). Magnetic Materials: Fundamentals and Applications (2nd ed.). Cambridge: Cambridge University Press. ISBN 9780521886697.
- Ibach, Harald; Lüth, Hans (2009). Solid-State Physics: An Introduction to Principles of Materials Science (4th extensively updated and enlarged ed.). Berlin: Springer. ISBN 9783540938033.
- Levy, Robert A. (1968). Principles of Solid State Physics. Academic Press. ISBN 978-0124457508.
- Fan, H. Y. (1987). Elements of Solid State Physics. Wiley-Interscience. ISBN 9780471859871.
- Dekker, Adrianus J. (1958). Solid State Physics. Macmillan. ISBN 9780333106235.
- Cusack, N. (1958). The Electrical and Magnetic Properties of Solids. Longmans, Green.
- Hall, J. R.; Hook, H. E. (1994). Solid State Physics (2nd ed.). Chichester: Wiley. ISBN 0471928054.
- Jullien, André; Guinier, Rémi (1989). The Solid State from Superconductors to Superalloys (Pbk. ed.). Oxford: Oxford Univ. Press. ISBN 0198555547.
- Mendelssohn, K. (1977). The Quest for Absolute Zero: The Meaning of Low Temperature Physics. with S.I. units. (2nd ed.). London: Taylor and Francis. ISBN 0850661196.
- Myers, H. P. (1997). Introductory Solid State Physics (2nd ed.). London: Taylor & Francis. ISBN 0748406603.
- Kittel, Charles (1996). Introduction to Solid State Physics (7th ed.). New York [u.a.]: Wiley. ISBN 0471111813.
- Palmer, John (2007). Planar Ising correlations (Online ed.). Boston: Birkhäuser. ISBN 9780817646202.
- Bertoldi, Dalía S.; Bringa, Eduardo M.; Miranda, E. N. (6 June 2012). "Analytical solution of the mean field Ising model for finite systems". Journal of Physics: Condensed Matter. 24 (22): 226004. Bibcode:2012JPCM...24v6004B. doi:10.1088/0953-8984/24/22/226004. Retrieved 12 February 2013.
- Brout, Robert (1965). Phase Transitions. New York, Amsterdam: W. A. Benjamin, Inc.
- Rau, C.; Jin, C.; Robert, M. (1 January 1988). "Ferromagnetic order at Tb surfaces above the bulk Curie temperature". Journal of Applied Physics. 63 (8): 3667. Bibcode:1988JAP....63.3667R. doi:10.1063/1.340679.
- Skomski, R.; Sellmyer, D. J. (1 January 2000). "Curie temperature of multiphase nanostructures". Journal of Applied Physics. 87 (9): 4756. Bibcode:2000JAP....87.4756S. doi:10.1063/1.373149.
- López Domínguez, Victor; Hernàndez, Joan Manel; Tejada, Javier; Ziolo, Ronald F. (8 January 2013). "Colossal Reduction in Curie Temperature Due to Finite-Size Effects in CoFe O Nanoparticles". Chemistry of Materials. 25 (1): 6–11. doi:10.1021/cm301927z.
- Bose, S. K.; Kudrnovský, J.; Drchal, V.; Turek, I. (1 November 2011). "Pressure dependence of Curie temperature and resistivity in complex Heusler alloys". Physical Review B. 84 (17). arXiv:1010.3025
 . Bibcode:2011PhRvB..84q4422B. doi:10.1103/PhysRevB.84.174422.
. Bibcode:2011PhRvB..84q4422B. doi:10.1103/PhysRevB.84.174422. - Webster, John G. (1999). The Measurement, Instrumentation, and Sensors Handbook (Online ed.). Boca Raton, FL: CRC Press published in cooperation with IEEE Press. ISBN 0849383471.
- Whatmore, R. W. (1991). Electronic Materials: From Silicon to Organics (2nd ed.). New York, NY: Springer. ISBN 978-1-4613-6703-1.
- Kovetz, Attay (1990). The Principles of Electromagnetic Theory (1st published. ed.). Cambridge, UK: Cambridge University Press. ISBN 0-521-39997-1.
- Hummel, Rolf E. (2001). Electronic Properties of Materials (3rd ed.). New York [u.a.]: Springer. ISBN 0-387-95144-X.
- Pascoe, K. J. (1973). Properties of Materials for Electrical Engineers. New York, N.Y.: J. Wiley and Sons. ISBN 0471669113.
- Paulsen, J. A.; Lo, C. C. H.; Snyder, J. E.; Ring, A. P.; Jones, L. L.; Jiles, D. C. (23 September 2003). "Study of the Curie temperature of cobalt ferrite based composites for stress sensor applications". IEEE Transactions on Magnetics. 39 (5): 3316–3318. doi:10.1109/TMAG.2003.816761. ISSN 0018-9464.
- Hwang, Hae Jin; Nagai, Toru; Ohji, Tatsuki; Sando, Mutsuo; Toriyama, Motohiro; Niihara, Koichi (21 January 2005). "Curie temperature Anomaly in Lead Zirconate Titanate/Silver Composites". Journal of the American Ceramic Society. 81 (3): 709–712. doi:10.1111/j.1151-2916.1998.tb02394.x.
- Sadoc, Aymeric; Mercey, Bernard; Simon, Charles; Grebille, Dominique; Prellier, Wilfrid; Lepetit, Marie-Bernadette (1 January 2010). "Large Increase of the Curie temperature by Orbital Ordering Control". Physical Review Letters. 104 (4). arXiv:0910.3393
 . Bibcode:2010PhRvL.104d6804S. doi:10.1103/PhysRevLett.104.046804.
. Bibcode:2010PhRvL.104d6804S. doi:10.1103/PhysRevLett.104.046804. - "Pierre Curie – Biography". Nobelprize.org, From Nobel Lectures, Physics 1901-1921, Elsevier Publishing Company, Amsterdam, 1967. The Nobel Foundation 1903. Retrieved 14 March 2013.
- Kochmański, Martin; Paszkiewicz, Tadeusz; Wolski, Sławomir (2013). "Curie–Weiss magnet: a simple model of phase transition". European Journal of Physics. 34: 1555–1573. arXiv:1301.2141
 . Bibcode:2013EJPh...34.1555K. doi:10.1088/0143-0807/34/6/1555.
. Bibcode:2013EJPh...34.1555K. doi:10.1088/0143-0807/34/6/1555.
External links
- Ferromagnetic Curie Point. Video by Walter Lewin, M.I.T.