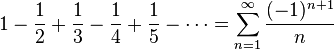Conditional convergence
In mathematics, a series or integral is said to be conditionally convergent if it converges, but it does not converge absolutely.
Definition
More precisely, a series 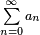 is said to converge conditionally if
is said to converge conditionally if
 exists and is a finite number (not ∞ or −∞), but
exists and is a finite number (not ∞ or −∞), but 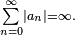
A classic example is the alternating series given by
which converges to 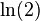 , but is not absolutely convergent (see Harmonic series).
, but is not absolutely convergent (see Harmonic series).
Bernhard Riemann proved that a conditionally convergent series may be rearranged to converge to any sum at all, including ∞ or −∞; see Riemann series theorem.
A typical conditionally convergent integral is that on the non-negative real axis of 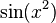 (see Fresnel integral).
(see Fresnel integral).
See also
References
- Walter Rudin, Principles of Mathematical Analysis (McGraw-Hill: New York, 1964).
This article is issued from Wikipedia - version of the 1/2/2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.