Cayley graph
In mathematics, a Cayley graph, also known as a Cayley colour graph, Cayley diagram, group diagram, or colour group[1] is a graph that encodes the abstract structure of a group. Its definition is suggested by Cayley's theorem (named after Arthur Cayley) and uses a specified, usually finite, set of generators for the group. It is a central tool in combinatorial and geometric group theory.
Definition
Suppose that is a group and is a generating set. The Cayley graph is a colored directed graph constructed as follows:[2]
- Each element of is assigned a vertex: the vertex set of is identified with
- Each generator of is assigned a color .
- For any the vertices corresponding to the elements and are joined by a directed edge of colour Thus the edge set consists of pairs of the form with providing the color.
In geometric group theory, the set is usually assumed to be finite, symmetric (i.e. ) and not containing the identity element of the group. In this case, the uncolored Cayley graph is an ordinary graph: its edges are not oriented and it does not contain loops (single-element cycles).
Examples
- Suppose that is the infinite cyclic group and the set S consists of the standard generator 1 and its inverse (−1 in the additive notation) then the Cayley graph is an infinite path.
- Similarly, if is the finite cyclic group of order n and the set S consists of two elements, the standard generator of G and its inverse, then the Cayley graph is the cycle . More generally, the Cayley graphs of finite cyclic groups are exactly the circulant graphs.
- The Cayley graph of the direct product of groups (with the cartesian product of generating sets as a generating set) is the cartesian product of the corresponding Cayley graphs.[3] Thus the Cayley graph of the abelian group with the set of generators consisting of four elements is the infinite grid on the plane , while for the direct product with similar generators the Cayley graph is the finite grid on a torus.


- A Cayley graph of the dihedral group D4 on two generators a and b is depicted to the left. Red arrows represent composition with a. Since b is self-inverse, the blue lines, which represent composition with b, are undirected. Therefore the graph is mixed: it has eight vertices, eight arrows, and four edges. The Cayley table of the group D4 can be derived from the group presentation
A different Cayley graph of Dih4 is shown on the right. b is still the horizontal reflection and represented by blue lines; c is a diagonal reflection and represented by green lines. As both reflections are self-inverse the Cayley graph on the right is completely undirected. This graph corresponds to the presentation
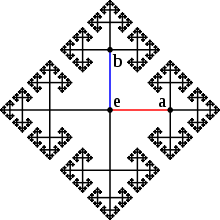
- The Cayley graph of the free group on two generators a, b corresponding to the set S = {a, b, a−1, b−1} is depicted at the top of the article, and e represents the identity element. Travelling along an edge to the right represents right multiplication by a, while travelling along an edge upward corresponds to the multiplication by b. Since the free group has no relations, the Cayley graph has no cycles. This Cayley graph is a key ingredient in the proof of the Banach–Tarski paradox.
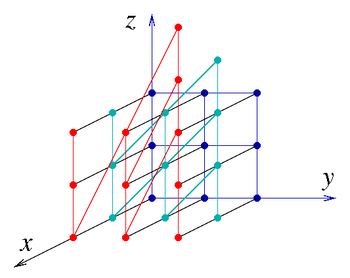
- A Cayley graph of the discrete Heisenberg group
is depicted to the right. The generators used in the picture are the three matrices X, Y, Z given by the three permutations of 1, 0, 0 for the entries x, y, z. They satisfy the relations , which can also be understood from the picture. This is a non-commutative infinite group, and despite being a three-dimensional space, the Cayley graph has four-dimensional volume growth.
Characterization
The group acts on itself by left multiplication (see Cayley's theorem). This may be viewed as the action of on its Cayley graph. Explicitly, an element maps a vertex to the vertex . The set of edges within the Cayley graph is preserved by this action: the edge is transformed into the edge . The left multiplication action of any group on itself is simply transitive, in particular, the Cayley graph is vertex transitive. This leads to the following characterization of Cayley graphs:
- Sabidussi Theorem: A graph is a Cayley graph of a group if and only if it admits a simply transitive action of by graph automorphisms (i.e. preserving the set of edges).[4]
To recover the group and the generating set from the Cayley graph , select a vertex and label it by the identity element of the group. Then label each vertex of by the unique element of that transforms into The set of generators of that yields as the Cayley graph is the set of labels of the vertices adjacent to the selected vertex. The generating set is finite (this is a common assumption for Cayley graphs) if and only if the graph is locally finite (i.e. each vertex is adjacent to finitely many edges).
Elementary properties
- If a member of the generating set is its own inverse, , then it is typically represented by an undirected edge.
- The Cayley graph depends in an essential way on the choice of the set of generators. For example, if the generating set has elements then each vertex of the Cayley graph has incoming and outgoing directed edges. In the case of a symmetric generating set with elements, the Cayley graph is a regular directed graph of degree
- Cycles (or closed walks) in the Cayley graph indicate relations between the elements of In the more elaborate construction of the Cayley complex of a group, closed paths corresponding to relations are "filled in" by polygons. This means that the problem of constructing the Cayley graph of a given presentation is equivalent to solving the Word Problem for .[1]
- If is a surjective group homomorphism and the images of the elements of the generating set for are distinct, then it induces a covering of graphs
- where
- In particular, if a group has generators, all of order different from 2, and the set consists of these generators together with their inverses, then the Cayley graph is covered by the infinite regular tree of degree corresponding to the free group on the same set of generators.
- A graph can be constructed even if the set does not generate the group However, it is disconnected and is not considered to be a Cayley graph. In this case, each connected component of the graph represents a coset of the subgroup generated by .
- For any finite Cayley graph, considered as undirected, the vertex connectivity is at least equal to 2/3 of the degree of the graph. If the generating set is minimal (removal of any element and, if present, its inverse from the generating set leaves a set which is not generating), the vertex connectivity is equal to the degree. The edge connectivity is in all cases equal to the degree.[5]
Schreier coset graph
If one, instead, takes the vertices to be right cosets of a fixed subgroup , one obtains a related construction, the Schreier coset graph, which is at the basis of coset enumeration or the Todd–Coxeter process.
Connection to group theory
Knowledge about the structure of the group can be obtained by studying the adjacency matrix of the graph and in particular applying the theorems of spectral graph theory.
Geometric group theory
For infinite groups, the coarse geometry of the Cayley graph is fundamental to geometric group theory. For a finitely generated group, this is independent of choice of finite set of generators, hence an intrinsic property of the group. This is only interesting for infinite groups: every finite group is coarsely equivalent to a point (or the trivial group), since one can choose as finite set of generators the entire group.
Formally, for a given choice of generators, one has the word metric (the natural distance on the Cayley graph), which determines a metric space. The coarse equivalence class of this space is an invariant of the group.
History
The Cayley Graph was first considered for finite groups by Arthur Cayley in 1878.[2] Max Dehn in his unpublished lectures on group theory from 1909–10 reintroduced Cayley graphs under the name Gruppenbild (group diagram), which led to the geometric group theory of today. His most important application was the solution of the word problem for the fundamental group of surfaces with genus ≥ 2, which is equivalent to the topological problem of deciding which closed curves on the surface contract to a point.[6]
Bethe lattice
The Bethe lattice or Cayley tree, is the Cayley graph of the free group on n generators. A presentation of a group G by n generators corresponds to a surjective map from the free group on n generators to the group G, and at the level of Cayley graphs to a map from the Cayley tree to the Cayley graph. This can also be interpreted (in algebraic topology) as the universal cover of the Cayley graph, which is not in general simply connected.
See also
- Vertex-transitive graph
- Generating set of a group
- Lovász conjecture
- Cube-connected cycles
- Algebraic graph theory
- Cycle graph (algebra)
Notes
- 1 2 Magnus, Wilhelm; Karrass, Abraham; Solitar, Donald (2004) [1966]. Combinatorial Group Theory: Presentations of Groups in Terms of Generators and Relations. Courier. ISBN 978-0-486-43830-6.
- 1 2 Cayley, Arthur (1878). "Desiderata and suggestions: No. 2. The Theory of groups: graphical representation". Amer. J. Math. 1 (2): 174–6. doi:10.2307/2369306. JSTOR 2369306. In his Collected Mathematical Papers 10: 403–405.
- ↑ Theron, Daniel Peter (1988), An extension of the concept of graphically regular representations, Ph.D. thesis, University of Wisconsin, Madison, p. 46, MR 2636729.
- ↑ Sabidussi, Gert (October 1958). "On a Class of Fixed-Point-Free Graphs". Proceedings of the American Mathematical Society. 9 (5): 800–4. doi:10.1090/s0002-9939-1958-0097068-7. JSTOR 2033090.
- ↑ See Theorem 3.7 of Babai, László (1995). "Chapter 27: Automorphism groups, isomorphism, reconstruction" (PDF). In Graham, R. L.; Grötschel, M.; Lovász, L. Handbook of Combinatorics. Amsterdam: Elsevier. pp. 1447–1540.
- ↑ Dehn, Max (2012) [1987]. Papers on Group Theory and Topology. Springer-Verlag. ISBN 1461291070. Translated from the German and with introductions and an appendix by John Stillwell, and with an appendix by Otto Schreier.