Category of relations

In mathematics, the category Rel has the class of sets as objects and binary relations as morphisms.
A morphism (or arrow) R : A → B in this category is a relation between the sets A and B, so R ⊆ A × B.
The composition of two relations R: A → B and S: B → C is given by:
- (a, c) ∈ S o R if (and only if) for some b ∈ B, (a, b) ∈ R and (b, c) ∈ S.[1]
Properties
The category Rel has the category of sets Set as a (wide) subcategory, where the arrow (function) f : X → Y in Set corresponds to the functional relation F ⊆ X × Y defined by: (x, y) ∈ F ⇔ f(x) = y.
The category Rel can be obtained from the category Set as the Kleisli category for the monad whose functor corresponds to power set, interpreted as a covariant functor.
Perhaps a bit surprising at first sight is the fact that product in Rel is given by the disjoint union (rather than the cartesian product as it is in Set), and so is the coproduct.
Rel is monoidal closed, with both the monoidal product A ⊗ B and the internal hom A ⇒ B given by cartesian product of sets.
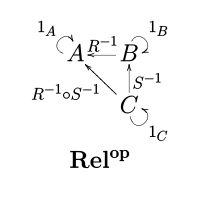
The involutory operation of taking the inverse (or converse) of a relation, where (b, a) ∈ R−1 : B → A if and only if (a, b) ∈ R : A → B, induces a contravariant functor Relop → Rel that leaves the objects invariant but reverses the arrows and composition. This makes Rel into a dagger category. In fact, Rel is a dagger compact category.
See also
- Allegory (category theory). The category of relations is the paradigmatic example of an allegory.