Pfister's sixteen-square identity
In algebra, Pfister's sixteen-square identity is a non-bilinear identity of form
![\begin{align}
& {}\quad (x_1^2+x_2^2+x_3^2+x_4^2+\cdots+x_{16}^2)(y_1^2+y_2^2+y_3^2+y_4^2+\cdots+y_{16}^2) \\[8pt]
& = z_1^2+z_2^2+z_3^2+z_4^2+\cdots+z_{16}^2
\end{align}](../I/m/a91ad82a9c441f204a41797c91a1ef51.png)
It was first proven to exist by H. Zassenhaus and W. Eichhorn in the 1960s,[1] and independently by Pfister[2] around the same time. There are several versions, a concise one of which is
If all 
with 
are set equal to zero, then it reduces to Degen's eight-square identity (in blue). The 
are
and,
The also obey,
Thus the identity shows that, in general, the product of two sums of sixteen squares is the sum of sixteen rational squares.
No sixteen-square identity exists involving only bilinear functions since Hurwitz's theorem states an identity of the form
with the 
bilinear functions of the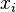 
and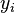 
is possible only for n ∈ {1, 2, 4, 8} . However, the more general Pfister's theorem (1965) shows that if the are just rational functions of one set of variables, hence has a denominator, then it is possible for all 
.[3] There are also non-bilinear versions of Euler's four-square and Degen's eight-square identities.
See also
References
- ↑ H. Zassenhaus and W. Eichhorn, "Herleitung von Acht- und Sechzehn-Quadrate-Identitäten mit Hilfe von Eigenschaften der verallgemeinerten Quaternionen und der Cayley-Dicksonchen Zahlen," Arch. Math. 17 (1966), 492-496
- ↑ A. Pfister, Zur Darstellung von -1 als Summe von Quadraten in einem Körper," J. London Math. Soc. 40 (1965), 159-165
- ↑ Pfister's Theorem on Sums of Squares, Keith Conrad, http://www.math.uconn.edu/~kconrad/blurbs/linmultialg/pfister.pdf